Сумма бесконечной геометрической прогрессии

Вопросы занятия:

·     рассмотреть бесконечную геометрическую прогрессию, модуль знаменателя которой меньше единицы;

·     вывести формулу для нахождения суммы такой прогрессии через предел последовательности.

Материал урока.

Прежде чем приступить к изучению нового материала, давайте выполним упражнение.

Упражнение.

Рассмотрим бесконечную геометрическую прогрессию и найдём сумму двух, трёх, четырёх и так далее членов прогрессии

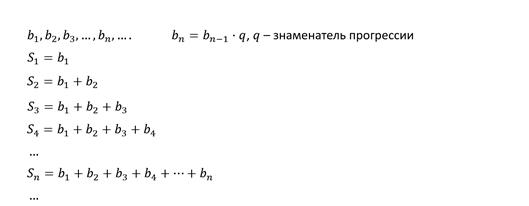
Получим последовательность:

Эта последовательность может сходится или расходится.

Если последовательность (S_n) сходится к пределу S, то число S называют суммой геометрической прогрессии. Обратите внимание, что мы не говорим суммой n членов геометрической прогрессии, а говорим суммой геометрической прогрессии.

Если же эта последовательность расходится, то о сумме геометрической прогрессии не говорят, хотя о сумме n первых членов прогрессии говорить можно.

Давайте вспомним и запишем формулу суммы эн первых членов геометрической прогрессии.

Рассмотрим случай, когда знаменатель q геометрической прогрессии по модулю меньше единицы.

Рассмотрим пример.

Пример.

Рассмотрим ещё один пример.

Пример.

Формулу суммы геометрической прогрессии используют для представления бесконечной десятичной периодической дроби в виде обыкновенной дроби.

Рассмотрим пример.

Пример.