Вопросы занятия:
· познакомиться с понятием асимптот;
· рассмотреть горизонтальные асимптоты;
· познакомиться с понятием предела функции на бесконечности.
Материал урока.
Прежде чем приступить к изучению темы, давайте выполним упражнение.
Упражнение.

В курсе базовой школы, при изучении графиков функции, мы с вами встречались с понятием асимптоты. Давайте вспомним, что это такое.
Определение:
Асимптота – это прямая, к которой график неограниченно приближается.
Напомним, что асимптоты бывают горизонтальные, вертикальные и наклонные.


Например, у гиперболы вертикальной асимптотой является ось Ox, а вертикальной – Oy.

Это не совсем строгое определение. Сегодня на уроке мы с вами дадим более строгое определение.
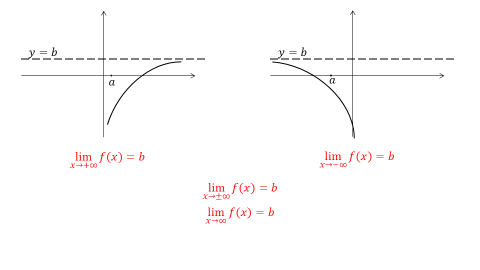
Пусть дана функция y = f(x), в области определения которой содержится луч от (a; + ∞) и пусть прямая y = b является горизонтальной асимптотой графика функции y = f(x). Тогда можно записать, что предел функции f(x) при x стремящемся к плюс бесконечности равен b.
Если же дана функция y = f(x), в области определения которой содержится луч (- ∞; a), и прямая y = b является горизонтальной асимптотой графика функции y = f(x), то можно записать, что предел функции f(x) при x стремящемся к минус бесконечности равен b.
Если одновременно выполняются оба соотношения, то можно записать, что предел функции f(x) при x стремящемся к плюс минус бесконечности равен b. Чаще всего знак плюс минус в данном равенстве убирают и просто говорят, что предел функции f(x) при x стремящемся к бесконечности равен b.
Рассмотрим пример.
Пример.

Для вычисления предела функции на бесконечности используют несколько утверждений. Давайте сформулируем их.

Рассмотрим несколько примеров.
Пример.

Пример.

Пример.
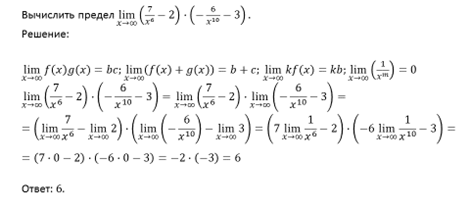

 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 7964
7964


