Решение неравенств с одной переменной

Вопросы занятия:

• на подробных примерах рассмотреть основные методы решения неравенств с одной переменной;

• повторить теоремы равносильности для неравенств;

• повторить определение «система неравенств» и «совокупность неравенств».

Материал урока

Сегодня на уроке мы постараемся обобщить все наши сведения о неравенствах, вспомним основные типы неравенств и основные методы решения неравенств с одной переменной.

Прежде всего, начнем с такого понятия как равносильность неравенств. Напомним, что решением неравенства f(x) > g(x) называют всякое значение переменной x, которое обращает данное неравенство в верное числовое неравенство.

Иногда можно встретить термин «частное решение». Множество всех частных решений неравенства называют общим решением, но чаще говорят просто «решение».

Дадим определение: два неравенства с одной переменной f(x) > g(x) и p(x) > h(x) называют равносильными, если их решения (или по другому – множество частных решений) совпадают.

Отметим, что знак больше в данных неравенствах необязателен, здесь может стоять любой знак неравенства как строгий так и нестрогий. Это же справедливо для всех утверждений, с которыми мы будем встречаться на сегодняшнем уроке.

Сформулируем еще одно определение: если решения неравенства f(x) > g(x) содержится в решении неравенства p(x) > h(x), то неравенство p(x) > h(x) называют следствием неравенства f(x) > g(x).

Например:

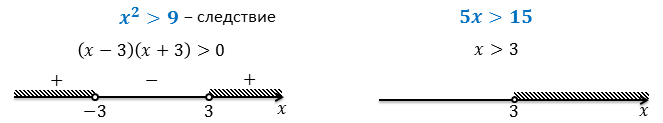
При решении уравнений получить уравнение следствие было не страшно, поскольку посторонние корни всегда можно было отсеять с помощью проверки. В неравенствах, как правило, решениями являются бесконечные множества чисел, поэтому доводить дело до проверки нецелесообразно. Поэтому при решении неравенств надо стараться выполнять только равносильные преобразования.

Как и при решении уравнений при решении неравенств пользуются шестью теоремами равносильностью.

Теорема 1. Если какой-либо компонент неравенства перенести из одной части неравенства в другую с противоположным знаком, оставив знак неравенства без изменения, то получится неравенство, равносильное данному.

Теорема 2. Если обе части неравенства возвести в одну и ту же нечетную степень, оставив знак неравенства без изменения, то получится неравенство, равносильное данному.

Теорема 3.

Теорема 4.

Теорема 5.

Теорема 6.

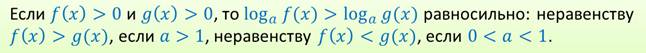
Прежде чем перейти к решению конкретных примеров, давайте вспомним определения систем и совокупностей неравенств и определим их отличия.

Определение.

Говорят, что несколько неравенств с одной переменной образуют систему неравенств, если ставится задача найти все такие значения переменной, каждое из которых является частным решением всех заданных неравенств. Значение переменной, при котором каждое из неравенств системы обращается в верное числовое неравенство, называют частным решением системы неравенств. Множество всех частных решений системы неравенств представляет собой общее решение системы неравенств (чаще говорят просто решение системы неравенств).

Решить систему неравенств – значит найти все ее частные решения. Решение системы неравенств представляет собой пересечение решений неравенств, образующих систему.

Говорят, что несколько неравенств с одной переменной образуют совокупность неравенств, если ставится задача найти все такие значения переменной, каждое из которых является решением хотя бы одного из заданных неравенств. Каждое такое значение переменной называют частным решением совокупности неравенств. Множество всех частных решений совокупности неравенств представляет собой решение совокупности неравенств.

Решение совокупности неравенств представляет собой объединение решений неравенств, образующих совокупность.

Неравенства, образующие систему, объединяются фигурной скобкой, а неравенства, образующие совокупность, – квадратной скобкой. Иногда неравенства, составляющие совокупность записывают в строчку, разделяя их точкой с запятой.

Рассмотрим пример.

Рассмотрим еще один пример.

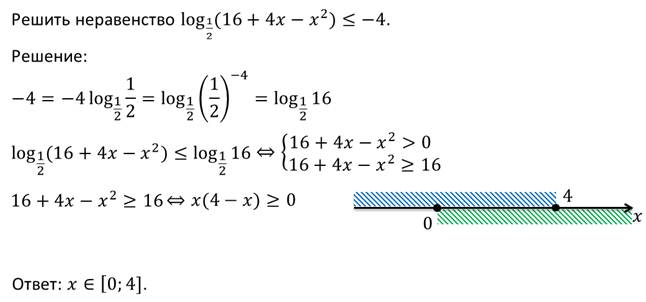
Рассматривая логарифмические неравенства, мы говорили, что при решении логарифмических неравенств переходят от неравенства:

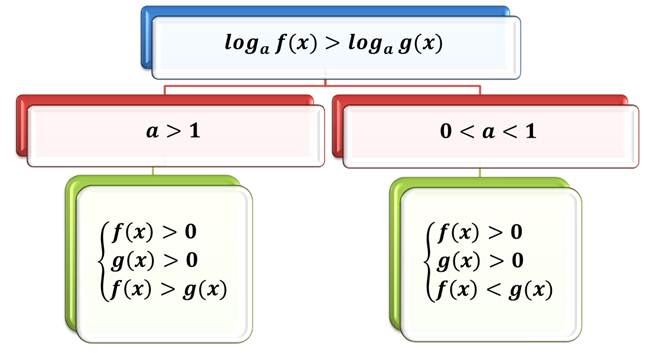
Первые два неравенства каждой из этих систем определяют ОДЗ переменной для исходного неравенства, а знак последнего неравенства каждой из систем либо совпадает со знаком исходного неравенства, в случае, когда а > 1, любо противоположен знаку исходного неравенства, в случае, когда 0 < а < 1.

Но, если посмотреть на эти системы внимательно, то можно заметить, что в каждой из составленных систем есть по одному «лишнему» неравенству.

Рассмотрим пример.

Теперь давайте рассмотрим иррациональные неравенства.

Запишем условие, определяющее ОДЗ:

При данных условиях обе части неравенства неотрицательны, значит, если по теореме 5 возвести их в квадрат, получим неравенство, равносильное данному.

Таким образом исходное иррациональное неравенство равносильно системе неравенств:

Рассмотрим неравенство:

Запишем условие, определяющее ОДЗ

Таким образом, данное иррациональное неравенство равносильно совокупности систем неравенств:

Рассмотрим пример:

Теперь давайте рассмотрим неравенства с модулями.

Рассмотрим пример.