Общие методы решения уравнений

Вопросы занятия:

• на примерах повторить основные методы решения уравнений.

Материал урока

Сегодня на уроке мы с вами вспомним основные методы решения уравнений. Первый метод, который мы вспомним, это метод замены уравнения h(f(x)) = h(g(x)) уравнением f(x) = g(x).

Применяют этот метод:

Этот метод можно применять только в том случае, когда функция y = h(x) – это монотонная функция, которая каждое свое значение принимает по одному разу.

Например

Это – равносильное преобразование уравнений.

Если же функция y = h(x) – немонотонная функция, то указанный метод применять нельзя, поскольку возможна потеря корней.

Например:

Следующим мы рассмотрим метод разложения на множители.

Суть этого метода:

После решения уравнений совокупности, нужно взять те корни, которые принадлежат области определения исходного уравнения, а остальные отбросить как посторонние.

Рассмотрим пример.

Рассмотрим еще один пример на применение метода разложения на множители.

Следующий метод – метод введения новой переменной.

Суть метода состоит в следующем:

Если вводится новая переменная, то полученное уравнение надо решать до конца, вплоть до проверки его корней, и только потом возвращаться к исходной переменной.

Рассмотрим пример.

Рассмотрим еще один пример.

Рассмотрим еще один пример.

Теперь рассмотрим пример, в котором использование этого метода не является очевидным.

Решить уравнение.

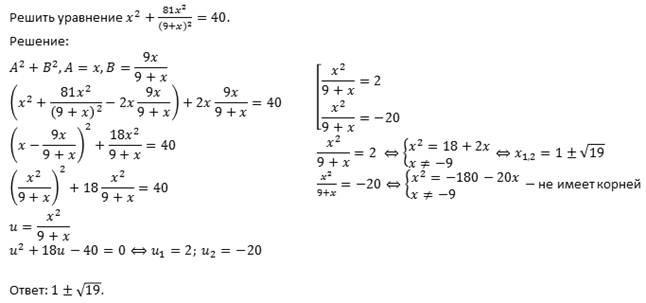
Рассмотрим еще один метод решения уравнений – функционально графический метод.

Суть этого метода:

Рассмотрим пример.

Рассмотрим еще один пример.

Рассмотрим пример.

Давайте, еще раз перечислим основные методы решения уравнений.