Уравнения и неравенства с двумя переменными

Вопросы занятия:

• повторить методы решения уравнений и неравенств с двумя переменными;

• рассмотреть примеры решения уравнений и неравенств с двумя переменными.

Материал урока

Прежде всего, вспомним, что называется решением уравнения с двумя переменными.

Определение.

Решением уравнения с двумя переменными p(x, y) = 0 называют всякую пару чисел (x; y), которая обращает уравнение в верное числовое равенство.

Например:

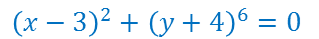
Поскольку в нашем уравнении присутствую четные степени, значит значение каждого слагаемого больше либо равно нулю. Сумма двух неотрицательных чисел равна нулю только тогда, когда каждое из слагаемых равно нулю.

Но так бывает далеко не всегда. Как правило, решений у уравнения с двумя переменными бесконечно много.

Например:

Переход к графику уравнения p(x, y) = 0– один из наиболее удобных приемов решения уравнения с двумя переменными.

Рассмотрим рациональное уравнение с несколькими переменными, с целочисленными коэффициентами.

Если поставлена задача - найти целочисленные решения, то говорят, что задано диофантово уравнение, названное в честь древнегреческого математика Диофанта.

Один из методов решения таких уравнений – с помощью теории делимости целых чисел.

Рассмотрим пример.

Давайте попробуем записать несколько частных решений этого уравнения. Для этого возьмем в качестве ка несколько конкретных целочисленных значений.

Рассмотрим еще один пример.

Рассмотрим еще один пример.

Теперь давайте поговорим о решении неравенств вида p (x, y) > 0, где p(x, y) – алгебраическое выражение.

Вместо знака больше в данном неравенстве может стоять любой знак неравенства как строгий так и нестрогий.

Напомним, что решением неравенства p(x, y) > 0 называют всякую пару чисел икс игрек, которая удовлетворяет этому неравенству, то есть обращает неравенство с переменными в верное числовое неравенство.

Например:

Чтобы найти все  решения неравенства с двумя переменными, чаще всего опираются на график уравнения p(x, y) = 0.

Рассмотрим пример.

Из курса базовой школы, мы помним, что если неравенство с двумя переменными строгое, то график функции изображается штриховой линией. Тогда все решения заданного неравенства геометрически изображаются точками полуплоскости, расположенной либо выше либо ниже построенной прямой. Чтобы правильно выбрать нужную полуплоскость, возьмем любую точку одной из них и подставим координаты этой точки в исходное неравенство. Если получится верное числовое неравенство, то полуплоскость выбрана верно, если нет, то неверно.

В предыдущем примере, мы нашли, что точка с координатами (2; 1) удовлетворяет исходному неравенству. Эта точка располагается выше прямой. Значит, геометрической моделью решений исходного неравенство является полуплоскость, расположенная выше прямой.

Еще раз обращаем внимание, что у нас строгое неравенство, поэтому сама линия в область решений не входит.

Рассмотрим еще один пример.

Теперь давайте рассмотри систему неравенств.

Решить систему неравенств с двумя переменными – это значит найти множество всех таких точек координатной плоскости, координаты которых удовлетворяют одновременно всем неравенствам системы.

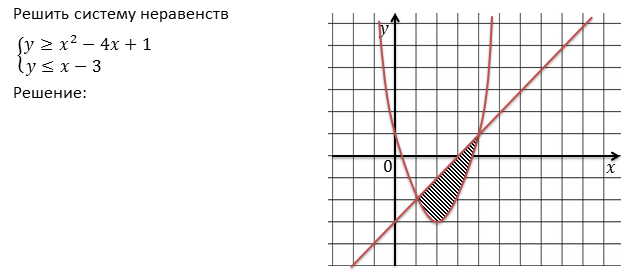
Рассмотрим пример.