Системы уравнений

Вопросы занятия:

• повторить методы решения уравнений и неравенств с двумя переменными;

• рассмотреть примеры решения уравнений и неравенств с двумя переменными.

Материал урока

В курсе алгебры базовой школы мы часто встречались с системами рациональных уравнений с двумя переменными. Решали эти системы мы с помощью следующих методов: метода подстановки, метода алгебраического сложения, метода введения новых переменных, графического метода.

Сначала давайте попробуем дать определение системе уравнений.

Определение.

Определение.

Пару значений (x; y), которая одновременно является решением и первого и второго уравнений системы, называют решением системы уравнений. Решить систему уравнений – значит найти все ее решения или установить, что решений нет.

Но совсем необязательно, чтобы в системе было два уравнения от двух переменных. Можно говорить о системе, содержащей любое число уравнений с любым числом переменных.

Мы уже говорили, что основная идея решения уравнений – переход от одного уравнения к другому, более простому, но равносильному данному. Если же получился переход к уравнению-следствию, то обязательна проверка найденных корней, поскольку среди них могут оказаться посторонние корни. Это же справедливо и для систем уравнений.

Определение.

Две системы уравнений называются равносильными, если они имеют одни и те же решения или если обе системы не имеют решений.

Рассмотрим пример.

Рассмотрим еще один пример.

Рассмотрим еще один пример.

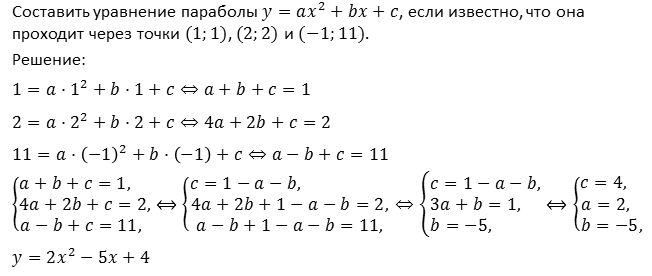
Рассмотрим еще один пример.