Знаковые модели. Математические модели

Математический язык является основным языком математического моделирования. Математическая модель – это информационная модель, которая построена с использованием математических понятий и формул.

Математический язык состоит из множества формальных языков. Со многими из них вы уже познакомились в школе (например алгебраический и геометрический), некоторые вы узнаете при дальнейшем обучении.

Существуют определённые требования к математическим моделям. Рассмотрим их. Первое требование – универсальность. Это означает, что в модели должны быть полностью отображены все изучаемые свойства реального объекта. Второе. Адекватность. В модели должны быть отражены все нужные свойства объекта с погрешностью не выше заданной. Третье. Точность. Совпадение характеристик реального объекта и значений этих характеристик, полученных с помощью моделей, должны быть максимально точными. Четвёртое требование. Экономичность. Данное требование определяется затратами ресурсов ЭВМ (памяти и времени) на её реализацию и эксплуатацию.

С помощью алгебраического языка можно формализовать функциональные зависимости между количественными характеристиками объекта моделирования. Функциональные зависимости вы можете найти в школьном курсе физики. Они представляют собой математические модели изучаемых процессов или явлений.

Разберёмся на примере. Зависимость количества теплоты при нагревании тела от разности конечной и начальной температуры имеет вид:

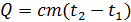
Зависимость силы тока от заряда, прошедшего через проводник за единицу времени выглядит следующим образом:

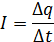
Так же с помощью языка алгебры логики строятся логические модели. При построении логической модели простые и сложные высказывания, выраженные, при помощи естественного языка формализуются, то есть записываются в виде логических выражений. При построении логических моделей можно решать логические задачи, создавать логические модели устройств и так далее.

Рассмотрим две электрические схемы соединения переключателей. На первой представлено последовательное соединение, а на второй – параллельное.

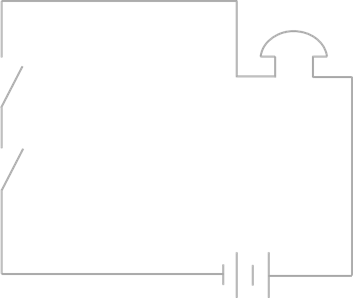
Схема последовательного соединения переключателей

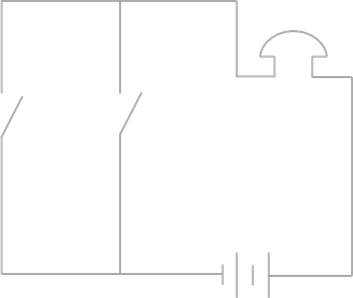
Схема параллельного соединения переключателей

На первой схеме, чтобы звонок зазвенел, должны быть включены оба переключателя.

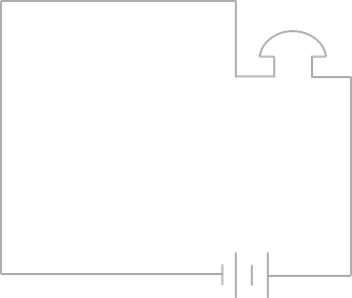
Схема последовательного соединения переключателей

На второй схеме достаточно, чтобы был включён хотя бы один из переключателей.

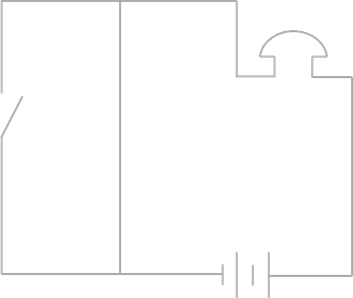
Схема параллельного соединения переключателей

Давайте проведём аналогию между элементами электрических схем, а также объектами и операциями алгебры логики и изобразим всё это в таблице.

Рассмотрим некоторые элементы нашей таблицы. Например, элемент электрической схемы «переключатель включён» в алгебре логики будет обозначаться как 1, а элемент «переключатель выключен» 0. Зададим вопрос: «Переключатель включён?». Если ответ на этот вопрос да (есть сигнал), то он будет обозначатся в алгебре логики как 1, если нет (нет сигнала), то 0.

Следующий элемент «последовательное соединение переключателей». Данный элемент подразумевает включение и первого и второго переключателя. В алгебре логики это называется конъюнкцией.

А если рассмотреть элемент «параллельное соединение переключателей», то в данном случае берётся включение одного из переключателей или обоих сразу. Таким образом достаточно, чтобы был включён хотя бы один из переключателей. В алгебре логики это называется дизъюнкцией.

Важно запомнить:

Математическая модель – это информационная модель, которая построена с использованием математических понятий и формул.

Требования к математическим моделям:

·      Универсальность;

·      Адекватность;

·      Точность;

·      Экономичность.

При построении логической модели формализуются (записываются в виде логических выражений) простые и сложные высказывания, выраженные при помощи естественного языка.