Знаковые модели. Компьютерные математические модели

Вопросы:

·      Определение компьютерной математической модели.

·      Использование компьютерной математических моделей.

·      Применение при решении задач.

Самые разные математические модели широко использовались и используются при изучении многих научных областей и дисциплин. Так, на пример, учёные астрономы используют математические модели, чтобы предсказать движение небесных тел. Как мы уже знаем, при составлении любых информационных моделей учитываются существенные свойства объекта или явления. Но что делать, если этих свойств очень много или они очень сложны для расчёта? Ведь человеку понадобится немало времени для реализации такой математической модели.

Реализация – это расчёт состояния объекта или системы, по формулам из математической модели, которые связывают значения его исходных и результирующих параметров.

Это одна из важнейших областей применения компьютеров. Ведь компьютер способен выполнять миллионы математических операций в секунду.

Математические модели, реализованные на компьютере с помощью тех или иных программных средств, называются компьютерными математическими моделями.

Для реализации математических моделей на компьютере могут использоваться:

·      различные языки программирования,

·      электронные таблицы,

·      различные математические пакеты.

При использовании некоторых средств визуализации можно наглядно представить результаты и процесс работы той или иной системы.

Компьютерные математические модели широко используются в различных областях науки. На пример, используя средства визуализации табличного процессора Microsoft Excel (его вы будете изучать позже) можно отобразить в виде линии траекторию полёта снаряда, который выпущен из пушки, расположенной на земле. Снаряд был выпущен с известной начальной скоростью, под определённым углом к горизонту.

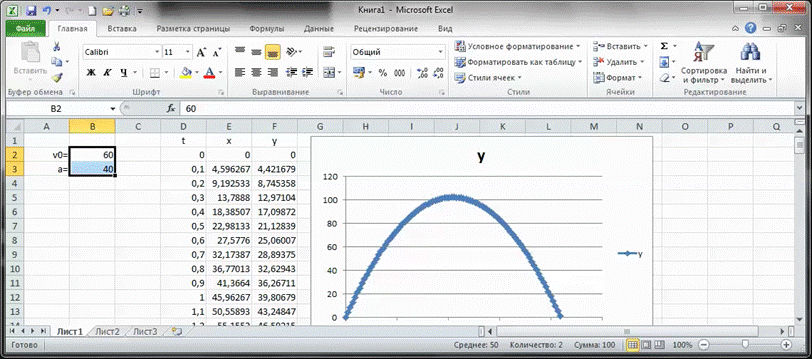
Реализация математической модели в Microsoft Excel

После того, как математическая модель была задана достаточно нескольких нажатий клавиш, чтобы изменить исходные данные системы. И мы тут же получили результирующие данные для системы с другими параметрами.

Особую роль среди компьютерных математических моделей занимают модели систем, параметры которых могут принимать случайные значения в определённых пределах. Часто для того, чтобы оптимизировать работу такой системы, моделируют её работу при различных параметрах и находят их оптимальные значения. Такая математическая модель называется имитационной.

Имитационные модели применяются во многих сферах жизни человека. Например, моделирование системы обслуживания покупателей в магазине, чтобы выяснить, какое количество продавцов необходимо для нормальной его работы. Ведь мы не можем точно предсказать количество покупателей, пришедших в магазин за единицу времени или точное время обслуживания продавцом каждого из них.

Подобные модели могут применяться во многих областях науки. Рассмотрим пример из теории вероятности. Хорошо известно, что вероятность выпадения герба или цифры при подбрасывании монеты равна 50%, но как это проверить? Можно много раз подбросить монету, записывая результат. При этом очевидно, что чем большее число подбрасываний мы совершим, тем результат будет точнее. Некоторые математики проделывали этот опыт. Результаты некоторые результаты представлены в таблице.

Мы видим, что при 4000 подбрасываний отклонение от предполагаемого результата составляет 0,8%. При этом такое количество подбрасываний монеты требует большого количества времени. Мы можем смоделировать нужное количество повторений опыта при помощи компьютера. Так даже миллион повторений займёт всего несколько секунд. Для моделирования нам достаточно взять величину, которая может принимать одно значение из двух. А затем раз за разом генерировать её случайное значение. В конце остаётся лишь найти процент выпадения одного значения от количества повторений опыта.

Одним из первых, кто предложил подход многократного прогона работы системы с различными параметрами при решении задач, был учёный-математик Станислав Улам. Такой подход породил целое семейство математических методов, назваными методами Монте-Карло.

Рассмотрим, как работает один из методов нахождения числа π. Вспомним, что числом π называется отношение длины окружности к длине её диаметра.

Для вычисления числа π можно представить следующую математическую модель. Нарисуем круг с центром в начале отсчёта. Будем использовать только ту часть круга, которая находится в первой координатной четверти. Впишем её в квадрат.

Очевидно, что длина стороны квадрата будет равна радиусу окружности.

Мы знаем, что площадь квадрата равна длине его стороны, возведённой в квадрат.

Площадь круга равна квадрату его радиуса, умноженному на π.

Тогда площадь четверти такого круга квадрату его радиуса, умноженному на π и делённому на 4.  

Поделив её на площадь квадрата, мы получим число π, делённое на четыре.

То есть для нахождения числа π нам достаточно найти отношение площади четверти круга к площади квадрата, в который она вписана. Но без использования числа π площадь четверти круга мы найти не можем. Возьмём случайную точку, находящуюся в заданном квадрате. Очевидно, что вероятность того, что случайная точка окажется в четверти круга, находясь при этом в квадрате равна отношению их площадей.

То есть для вычисления числа π нам достаточно найти вероятность попадания точки в четверть круга и умножить её на четыре.

Для того, чтобы найти эту вероятность как можно точнее нужно взять как можно больше таких случайных точек и найти отношение количества точек, попавших в четверть круга к общему их числу.

Узнать попала ли точка в четверть круга, можно найдя её расстояние от начала отсчёта. Для этого можно использовать следующую формулу.

Затем необходимо сравнить её с радиусом круга. Если расстояние больше радиуса – точка не в круге.

Очевидно, что использование компьютерной модели помогает получить больший объем данных о результатах работы системы за короткое время. Если мы возьмём десять миллионов точек, то для того, чтобы определить, попала ли каждая из них в четверть круга, человеку понадобится около девятнадцати лет непрерывного труда. А компьютеру для того, чтобы рассчитать такой объем информации, достаточно пяти минут.

Важно запомнить:

·      Компьютерные математические модели – это математические модели, которые реализованы на компьютере с помощью программных средств.

·      Компьютерные математические модели могут быть реализованы с помощью разных языков программирования, электронных таблиц и некоторых математических пакетов.

·      Имитационные компьютерные модели – это модели, которые воспроизводят работу различных систем, параметры которых могут принимать случайные значения.

·      Так же мы рассмотрели некоторые примеры компьютерных моделей.