Вопросы занятия:
· сформулировать и доказать свойства корня n-ой степени из неотрицательного числа, в случае натурального n;
· рассмотреть примеры использования этих свойств на примерах.
Материал урока
Прежде чем перейти к изучению нового материала, давайте повторим основные понятия, с которыми мы познакомились на предыдущих уроках.
Корнем n-ой степени из неотрицательного числа a называют такое неотрицательное число, при возведении которого в степень n получается число а.
Корнем нечётной степени n-ой из отрицательного числа а называют такое отрицательное число, при возведении которого в степень n получается а.
Обозначают:

Число а – это подкоренное число, число n – показатель корня.
На сегодняшнем уроке мы рассмотрим основные свойства операции извлечения корня n-ой степени.
Итак, первое свойство формулируется следующей теоремой.
Теорема 1.
Корень n-ой степени (где n = 2, 3, 4, …) из произведения двух неотрицательных чисел равен произведению корней n-ой степени из этих чисел.

Доказательство.
Введём следующие обозначения:

Нам надо доказать, что для неотрицательных чисел x, y, z выполняется равенство x = yz.
Из определения корня n-ой степени из неотрицательного числа мы знаем:

После замены в равенстве чисел a, b, произведения ab на соответствующие им выражения, получим, что:

Что и требовалось доказать.
Очевидно, что теорема остаётся справедливой и для случая, когда подкоренное выражение представляет собой произведение более чем двух неотрицательных чисел.
Рассмотрим следующее свойство.
Сформулируем теорему.
Теорема 2.
Если a ≥ 0, b>0 и n – натуральное число, n > 1, то справедливо равенство:

Доказательство.
Доказывать это свойство мы будем аналогично предыдущему. Введём обозначения.

Используя определение корня n-ой степени из неотрицательного числа, можно записать:

Получим:

Что и требовалось доказать.
Давайте рассмотрим несколько примеров.
Пример.

Пример.

Рассмотрим ещё одно свойство корня n-ой степени из неотрицательного числа.
Теорема 3.
Если a ≥ 0, k – натуральное число и n – натуральное число, n > 1, то справедливо равенство:

Другими словами, чтобы возвести корень в натуральную степень достаточно возвести в эту степень подкоренное выражение.
Доказательство.
Эта теорема является следствием теоремы 1. Если k = 3, то получим:

Точно так же можно рассуждать в случае любого другого натурального значения показателя k.
Рассмотрим ещё одно свойство.
Теорема 4.
Если a ≥ 0, k – натуральное число и n – натуральное число, n > 1, то справедливо равенство:

Доказательство этого свойства вы можете провести самостоятельно, оно аналогично доказательству первой и второй теоремы.
Мы с вами научились перемножать, делить, возводить в степень и извлекать корень из корней n-ой степени из неотрицательного числа. А как же складывать и отнимать такие корни? Никак. Их нельзя просто так складывать и вычитать. Надо преобразовывать каждый корень, а затем, если это возможно, складывать полученные результаты.
Рассмотрим это на примере.
Пример.
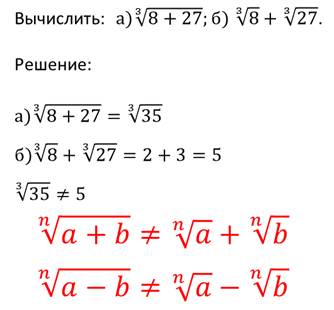
Рассмотрим ещё одно свойство корней n-ой степени из неотрицательных чисел.
Теорема 5.
Если показатели корня и степени подкоренного выражения умножить или разделить на одно и то же натуральное число, то значение корня не изменится.

Например.

Доказательство.
Введём некоторые обозначения:

Тогда по определению корня n-ой степени из неотрицательного числа, можно записать:

Возведём обе части последнего равенства в одну и ту же степень p, получим:

Итак, получили:

Что и требовалось доказать.
Рассмотрим несколько примеров.
Пример.

Пример.

Пример.
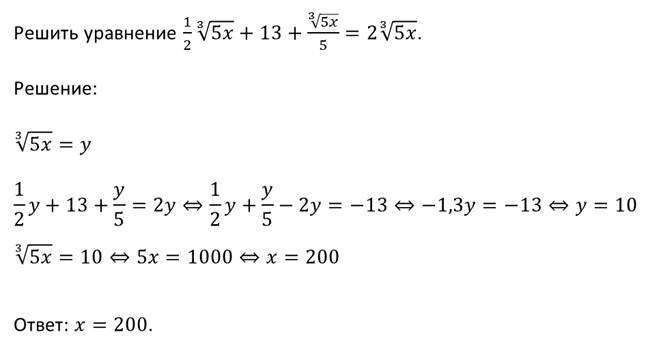
Пример.

Давайте запишем свойства корней энной степени из неотрицательного числа ещё раз:

Обратите внимание, что мы рассматривали с вами свойства корней n-ой степени только из неотрицательных чисел. Потому что корень n-ой степени из отрицательного числа имеет смысл только при нечётных n. Для таких значений показателей корня рассмотренные свойства корней верны и в случае отрицательных подкоренных выражений.
Рассмотрим пример.


 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 18904
18904


