Преобразование выражений, содержащих радикалы

Вопросы занятия:

·     ввести понятие «радикал»;

·     рассмотреть примеры, в которых выполняются преобразования выражений с радикалами.

Материал урока

На прошлых уроках мы с вами познакомились с корнем n-ой степени из а, рассмотрели основные свойства корня. На сегодняшнем уроке мы будем решать задачи на преобразование выражений с радикалами, используя все, что мы изучали на предыдущих уроках.

Повторим основные понятия.

Корнем n-ой степени из неотрицательного числа a называют такое неотрицательное число, при возведении которого в степень n получается число а.

Корнем нечётной степени n-ой из отрицательного числа а называют такое отрицательное число, при возведении которого в степень n получается а.

Обозначают:

Число а – это подкоренное число, число n – показатель корня.

Перечислим основные свойства

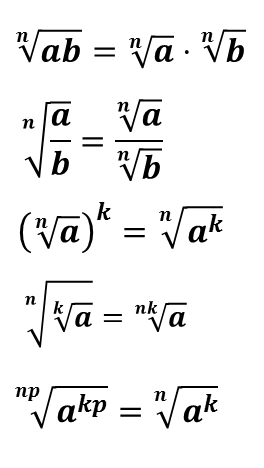
Прежде чем приступить к решению упражнений, давайте отметим некоторые важные моменты.

Верно ли что:

Нет, так как, например:

Верно ли что:

Нет, так как, например:

В данном случае справедлива формула:

Эта же формула справедлива для любого чётного показателя степени.

Для нечётного показателя степени имеем другую формулу.

Рассмотрим несколько примеров.

Пример.

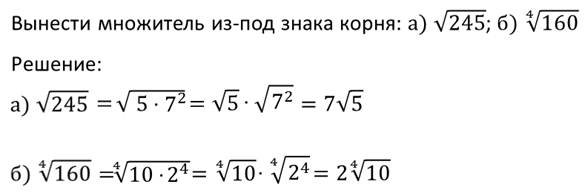
Пример.

Пример.

Пример.

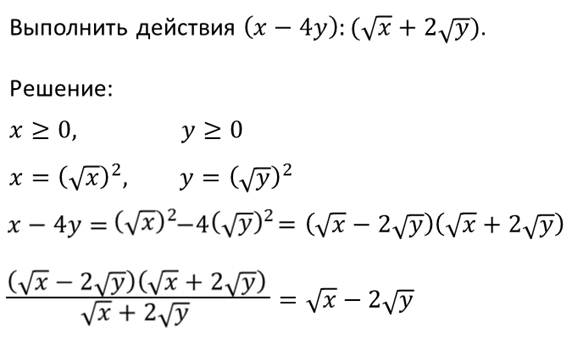
Пример.

Пример.

Пример.

Пример.

Пример.

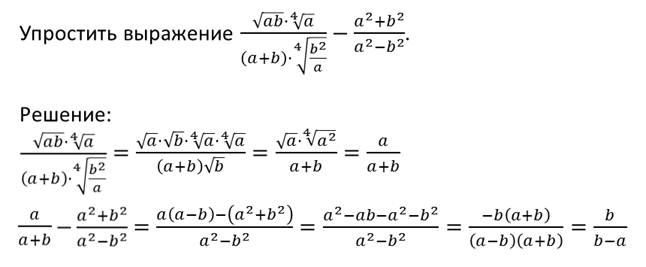
Пример.

Ещё раз хотелось бы обратить ваше внимание, что решая задачи с радикалами, в первую очередь мы должны обратить внимание на то, какой знак может иметь подкоренное выражение. И только после этого приступать к преобразованию выражений.