Обобщение понятия о показателе степени

Вопросы занятия:

·  обобщить случаи, когда показатель степени – рациональное или целое число;

·  ввести понятие «иррациональных уравнений».

Материал урока

На сегодняшнем уроке мы постараемся объединить все, что мы знаем о показателе степени, вспомним все свойства степеней в зависимости от показателя.

Прежде всего, давайте вспомним, что такое степень.

Определение.

Степень с натуральным показателем – произведение n множителей, каждый из которых равен а.

В записи aⁿ: а – это основание степени, n – это показатель степени.

Напомним, что:

Все это мы изучали с вами раньше. А теперь давайте рассмотрим степень, показателем которой является не натуральное, а рациональное число.

Определение.

Рациональным числом называется число, которое можно представить в виде обыкновенной дроби m/n, где m – это целое число, а n – натуральное. То есть на сегодняшнем уроке мы познакомимся с:

Запишем определение.

Определение.

Почему ввели ограничение q ≠ 1? Потому что при q = 1 показатель степени становится целым числом. А все свойства таких степеней мы уже рассматривали раньше.

Запишем несколько степеней и преобразуем их в радикалы.

При таком определении степени с рациональным показателем сохраняются все привычные свойства степеней, которые были доказаны для натуральных показателей:

Используя свойства таких степеней, становится проще делать некоторые преобразования радикалов.

Рассмотрим несколько примеров.

Пример.

Пример.

Давайте теперь рассмотрим степень с рациональным показателем в случае отрицательного показателя.

Например:

Для таких степеней справедливы те же свойства, что и для степеней с положительным рациональным показателем.

Давайте запишем их ещё раз:

Рассмотрим несколько примеров.

Пример.

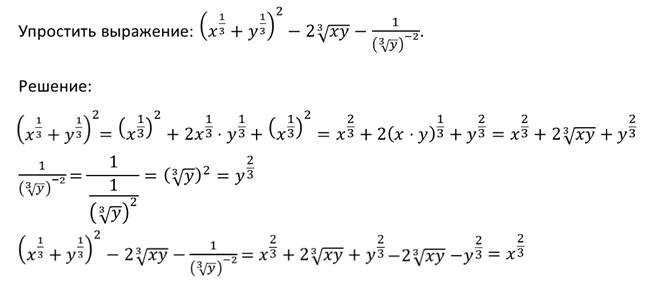
Пример.

Определение.

Уравнения, в которых переменная содержится под знаком корня или возводиться в дробную степень, называют иррациональными.

С такими уравнениями вы уже встречались в курсе алгебры 8 класса. Напомним основные методы решения иррациональных уравнений.

Метод возведения обеих частей уравнения в одну и ту же степень.

Метод введения новых переменных.

Функционально-графический метод.

Более подробно иррациональные уравнения и методы их решения мы рассмотрим позднее.