Степенные функции, их свойства и графики

Вопросы занятия:

·     рассмотреть степенные функции;

·     рассмотреть свойства и графики степенных функций, в зависимости от основания.

Материал урока

Определение.

Степенными функциями называют функции вида:

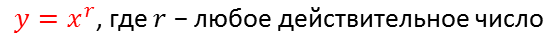
Случаи, когда r – натуральное или целое число мы с вами уже изучали.

Давайте повторим основные моменты.

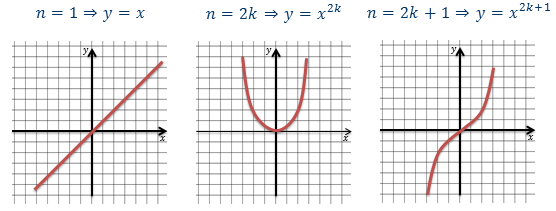
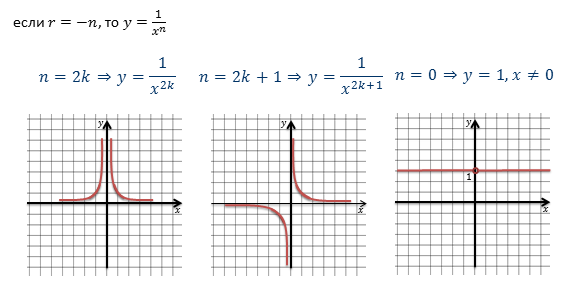
Сегодня на уроке мы познакомимся с функцией:

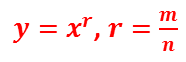
Для начала рассмотрим случай, когда показатель степени больше 0. Этот случай можно разбить ещё на два: когда показатель степени находится в (0; 1) и когда показатель степени больше 1.

Первым рассмотрим случай, когда показатель степени находится в промежутке (0; 1).

Рассмотрим частный случай такой степенной функции:

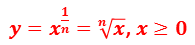
Как выглядит график этой функции, мы знаем.

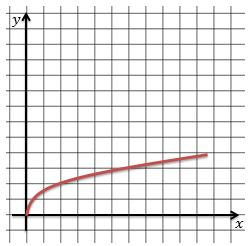
Точно так же будут выглядеть графики любой степенной функции вида:

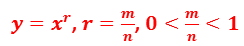
По графику мы очень просто можем записать основные свойства таких функций.

Областью определения будет являться луч [0; +∞).

Областью значения является промежуток [0; +∞).

Функция не является ни чётной, ни нечётной.

Функция возрастает на всей области определения.

Она не ограничена сверху, но ограничена снизу.

Наименьшее значение равно 0, а наибольшего значения нет.

Функция непрерывна на всей области определения.

График функции выпуклый вверх на всей области определения.

Теперь рассмотрим степенную функцию, показатель которой – любое рациональное число больше единицы.

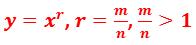
Графиком функции будет ветвь параболы, проходящая через точки (0; 0) и (1; 1), причём чем больше показатель, тем круче будет идти график.

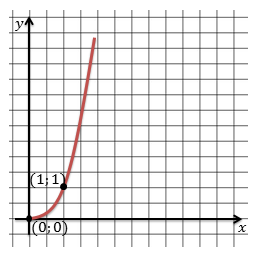
Запишем основные свойства функции.

Областью определения является луч [0; +∞).

Область значений – это промежуток (0; +∞).

Функция не является ни чётной, ни нечётной.

Функция возрастает на всей области определения.

Функции не ограничена сверху, но ограничена снизу.

Наименьшим значением будет 0, наибольшего значения нет.

Функция непрерывна на всей области определения.

График функции выпуклый вниз на всей области определения.

Теперь рассмотрим функцию:

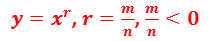
Сегодня мы уже с вами вспоминали как выглядит график функции y = x^-n, в случае натурального эн. Поскольку степень с рациональным отрицательным показателем рассматривается на интервале (0; +∞), то график функции y = x^r, если r – это отрицательное рациональное число будет похож на ветвь гиперболы и проходить через точку (1; 1).

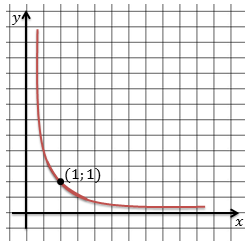
График имеет горизонтальную асимптоту игрек равно нулю и вертикальную асимптоту икс равно нулю.

Запишем основные свойства функции.

Областью определения будет промежуток (0; +∞).

Областью значения будет промежуток (0; +∞).

Функция не является ни чётной, ни нечётной.

Функция убывает на всей области определения.

Функция ограничена снизу, но не ограничена сверху.

Функция не имеет ни наибольшего ни наименьшего значения.

Функция непрерывна на всей области определения.

График функции выпуклый вниз на всей области определения.

Обратите внимание, что при рассмотрении функций мы нигде не проверяли функцию на дифференцируемость. Прежде чем говорить о дифференцируемости давайте посмотрим, как находится производная таких функций.

Производную функции игрек равно x в натуральной степени эн мы знаем, это табличное значение.

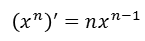
Чему равна производная функции x^-n, в случае натурального n, найти нетрудно:

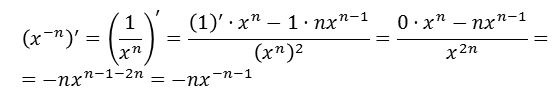
Эти две формулы можно объединить в одну:

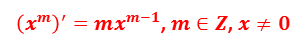
Ещё одним табличным значением является производная функции:

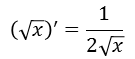
Эту формулу можно записать следующим образом:

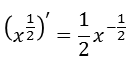
Теорема.

Если x > 0 и r – любое рациональное число, то производная степенной функции y = x^r вычисляется по формуле:

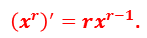
Поскольку производные данных функции существуют на всей области определения, то в свойства можно дописать, что функции дифференцируемы на всей области определения.

Рассмотрим несколько примеров.

Пример.

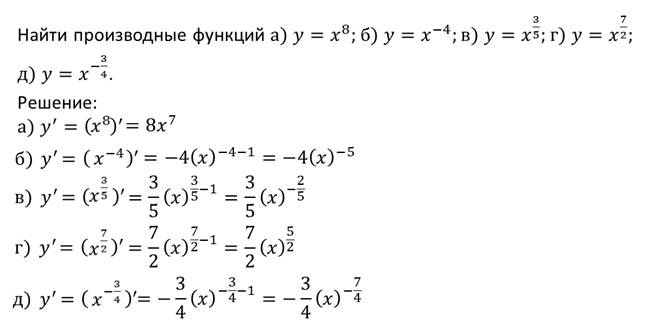
Пример.

Пример.

Пример.

Давайте повторим ещё раз основные свойства и графики функций.