Получите свидетельство
Вход
Вопросы занятия:
· рассмотреть свойства функции корень n-ой степени из x;
· рассмотреть график функции корень n-ой степени из x;
· рассмотреть примеры на построение и нахождение свойств функций этого вида.
Материал урока
Прежде чем перейти к изучению нового материала, давайте повторим основные понятия, с которыми мы познакомились на предыдущих уроках.
Корнем n-ой степени из неотрицательного числа a называют такое неотрицательное число, при возведении которого в степень n получается число а.
Корнем нечётной степени n-ой из отрицательного числа а называют такое отрицательное число, при возведении которого в степень n получается а.
Обозначают:
Число а – это подкоренное число, число n – показатель корня.
Обобщая эти понятия, можно сказать, что из любого неотрицательного числа можно извлечь корень любой степени (второй, третьей, четвертой и так далее), а из отрицательного числа можно извлечь только корень нечётной степени.
То есть на [0; +∞) каждому числу x можно поставить в соответствие единственное число корень n-ой степени из x при любом значении n.
Другими словами, на множестве [0; +∞) можно говорить о функции:
Давайте попробуем найти свойства этой функции и построить её график.
Основные свойства:
Областью определения будет являться промежуток [0; +∞).
Поскольку корнем n-ой степени из неотрицательного числа является неотрицательное число, то областью значений функции будет промежуток [0; +∞).
Поскольку область определения функции не является симметричным множеством, то функция не является ни чётной, ни нечётной.
Операцию извлечения корня мы вводили как операцию обратную возведению в соответствующую степень.
Тогда можно сказать, что:
Зная это, нетрудно построить график функции.
Используя построенный график, мы можем записать оставшиеся свойства функции.
Функция возрастает на промежутке [0; +∞).
Функция не ограничена сверху, но ограничена снизу, например, прямой y = -0,5.
Наименьшим значением функции будет 0, наибольшего значения функция не имеет.
Функция непрерывна на всей области определения.
Функция выпукла вверх на всей области определения.
При изучении темы дифференцирование функций, мы говорили, что если функция дифференцируема в каждой точке некоторого промежутка, то она непрерывна на данном промежутке. Из курса базовой школы мы знаем:
Тогда:
Эта производная существует в любой точке промежутка [0; +∞) за исключением точки 0.
Таким образом, функция имеет производную в любой точке промежутка (0; +∞), то есть функция дифференцируема на промежутке (0; +∞).
Рассмотрим несколько примеров.
Пример.
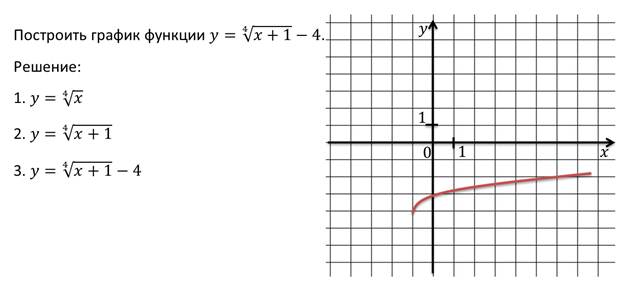
Пример.
Мы с вами говорили о функции y равно корень n-ой степени из x только для неотрицательных значений аргумента.
Но если эн нечётное число, то выражение корень n-ой степени из x имеет смысл и для отрицательных x. Значит, можно говорить о функции:
Теперь давайте запишем свойства этой функции.
Областью определения будет промежуток (– ∞; + ∞).
Областью значений будет промежуток (– ∞; + ∞).
Поскольку область определения является симметричным множеством, то можно исследовать данную функцию на чётность:
Получаем, что функция при нечётном n будет нечётной.
Давайте построим график функции.
Воспользуемся свойством нечётности функции и добавим к этой ветви ветвь, симметричную ей относительно начала координат.
По графику легко записать оставшиеся свойства функции.
Функция возрастает на всей области определения.
Функция не ограничена ни сверху ни снизу.
Функция не имеет ни наименьшего, ни наибольшего значений.
Функция непрерывна на всей области определения.
Функция выпукла вниз на промежутке (– ∞; 0) и выпукла вверх на промежутке (0; + ∞).
Функция дифференцируема на всей области определения за исключением точки 0.
Рассмотрим несколько примеров.
Пример.
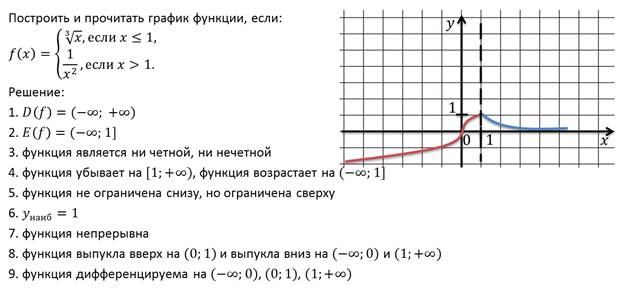
Пример.
Пример.
1
37170
спасибо