Понятие корня n - степени из действительного числа

Вопросы занятия:

·     ввести понятие корня n-ой степени из неотрицательного числа a;

·     ввести понятие корня нечётной степени n-ой степени из отрицательного числа a.

Материал урока

Давайте решим уравнение:

x⁴ = 1

Решим его алгебраическим способом. Перенесём все слагаемые в левую часть, применим формулу разности квадратов и получим, что исходное уравнение разбивается на два уравнения:

x² – 1 = 0 или x² + 1 = 0

Легко увидеть, что второе уравнение не имеет решений, в первом уравнении применим формулу разности квадратов и получим, что корнями данного уравнения являются числа:

x₁ = -1

x₂ = 1

Решим это же уравнение графически. Изобразим на одной координатной плоскости графики функций y = x⁴ и y = 1.

Графики этих функций пересекаются в двух точках:

Давайте с помощью этого же графика попробуем решить уравнение x⁴ = 16.

Легко увидеть, что решениями данного уравнения будут числа 2 и -2.

А теперь давайте попробуем решить уравнение x⁴ = 7.

Мы видим, что у данного уравнения будет два корня, одинаковых по модулю, но противоположных по знаку.

Таких, что при возведении в 4 степень получится число 7. Но как же их найти? Точных значений с помощью графика получить практически невозможно. Мы можем только сказать, что эти значения будут находится, в (1; 2) и (-2; -1).

Как бы мы не уменьшали масштаб и не уточняли график функции, точного значения этих корней мы не получим. На множестве целых чисел таких чисел нет, их нет и на множестве рациональных чисел. Эти числа будут представлять собой бесконечные непериодические дроби. Из курса алгебры базовой школы, мы знаем, что такие числа называются иррациональными.

То есть решениями данного уравнения являются два иррациональных числа. Для таких случаев учёными был введён в рассмотрение символ

С помощью этого символа корни уравнения x⁴ = 7 можно записать так:

Теперь давайте решим уравнение x³ = 5. Решать это уравнение мы будем графически. Изобразим в одной координатной плоскости графики функций: y = x³ и y = 5.

По графику видно, что решением будет одно число:

С помощью введённого понятия, можно записать, что корень данного уравнения равен:

Обобщая выше рассмотренные примеры, можно сказать, что:

Обратите внимание, что у нас слово корень применяется к нескольким понятиям: как корень уравнения и как корень n-ой степени из числа.

Теперь давайте дадим чёткое определение корня n-ой степени из числа а.

Определение:

Корнем n-ой степени из неотрицательного числа a называют такое неотрицательное число, при возведении которого в степень n получается число а.

Это число обозначают

Число а – это подкоренное число, а число n – это показатель корня.

Для некоторых корней энной степени введены специальные названия. Так корень второй степени называют просто квадратный корень и пишут так:

Этот частный случай вы изучали в восьмом классе.

Если n = 3, то вместо корень третьей степени говорят кубический корень. С кубическим корнем, вы тоже уже знакомы.

Операцию нахождения корня из неотрицательного числа называют извлечением корня. Эта операция является обратной по отношению к возведению в соответствующую степень.

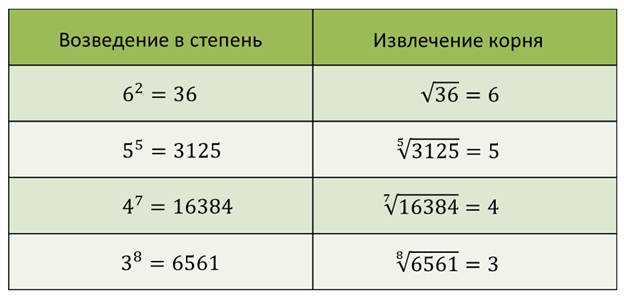
Обратите внимание, что в таблице мы рассматриваем только положительные числа, как это и сформулировано в определении.

Выражение:

называют радикалом (от латинского слова радикс, что означает «корень»).

Рассмотрим несколько примеров.

Пример.

Операцию извлечения корня можно определить и для отрицательного подкоренного числа, но только в случае нечётного показателя корня. Другими словами:

При этом используется следующее определение.

Определение:

Корнем нечётной степени n-ой из отрицательного числа а называют такое отрицательное число, при возведении которого в степень n получается а.

Это число также обозначают:

Число а – это подкоренное число, число n – показатель корня.

Обобщая все определения, можно сказать, что корень чётной степени имеет смысл только для неотрицательного подкоренного числа; корень нечётной степени имеет смысл для любого подкоренного числа.

Рассмотрим несколько примеров.

Пример.

Пример.

Пример.

Пример.

Давайте ещё раз повторим понятия и определения, с которыми мы познакомились на этом уроке.

Корнем n-ой степени из неотрицательного числа a называют такое неотрицательное число, при возведении которого в степень n получается число а.

Корнем нечётной степени n-ой из отрицательного числа а называют такое отрицательное число, при возведении которого в степень n получается а.

Обозначают:

Число а – это подкоренное число, число n – показатель корня.