Изобразим
произвольные векторы  и
и
 .
.
Далее
от некоторой точки О отложим векторы  и
и
 ,
равные векторам
,
равные векторам  и
и

соответственно.
Тогда угол АОB будет являться углом
между векторами  и
и
 .
.
Обозначим градусную меру угла АОB за α.
Говорят,
что угол между векторами  и
и
 равен
α.
равен
α.
Если
выбрать некоторую точку О1 и отложить от неё векторы  и
и
 ,
равные соответственно векторам
,
равные соответственно векторам  и
и
 ,
то полученный угол А1О1B1
будет равен углу АОB. Значит, и их
градусные меры тоже равны.
,
то полученный угол А1О1B1
будет равен углу АОB. Значит, и их
градусные меры тоже равны.
Отсюда можем сделать вывод, что величина α не зависит от выбора точки, от которой будут отложены векторы.
Угол
между векторами  и
и
 будем
обозначать так.
будем
обозначать так.

Величина его равна α.
Например,
угол между векторами  и
и
 равен
25°. Угол между векторами
равен
25°. Угол между векторами  и
и
 —
70°. Угол между векторами
—
70°. Угол между векторами  и
и
 равен
110°.
равен
110°.

Далее рассмотрим несколько частных случаев.
Первой будет пара коллинеарных сонаправленных векторов. Видим, что угол между ними равен нулю.

Так же угол между векторами равен 0, если один из них является нулевым или оба вектора нулевые. Ведь нулевой вектор сонаправлен любому, а значит, эти случаи можно отнести к первому, где рассматривались сонаправленные векторы.
Теперь рассмотрим пару противоположно направленных векторов, отложенных от одной точки.
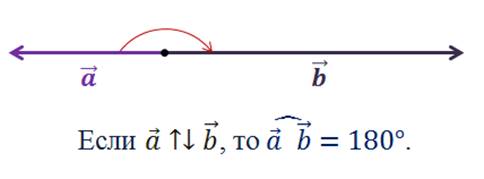
Видим, что угол между ними равен 180°.
Ещё одним частным случаем являются векторы, угол между которыми равен 90°. Такие векторы называют перпендикулярными.
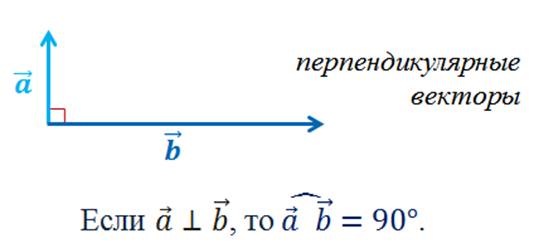
Ранее мы с вами рассматривали также углы между прямыми. Вы должны помнить, что они всегда были острыми.
В случае с векторами, угол между ними может быть как острым, так и тупым, но не больше 180°.
Можно
записать, что величина угла между векторами  .
.
Задача.
 равносторонний.
Найти:
равносторонний.
Найти:
а)
 ,
,
 ;
б)
;
б)  ,
,
 ;
в)
;
в)  ,
,
 .
.
Решение.

а)


б)


в)


Выполнив это задание, мы убедились в том, что угол между векторами лежит в пределах от 0 до 180° в отличие от угла между двумя прямыми.
Задача.
Среди векторов  ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 указать
пары перпендикулярных векторов, лежащих в одной грани прямоугольного
параллелепипеда
указать
пары перпендикулярных векторов, лежащих в одной грани прямоугольного
параллелепипеда  .
.

1)

2)

3)

4)

5)

Далее решим задачу.
Задача.
Меньшая диагональ  ромба
ромба
 равна
его стороне. Найти:
равна
его стороне. Найти:
а)
 б)
б)  в)
в)  г)
г)  д)
д)  е)
е) 
Решение.

а)

б)

в)

г)

д)

е)

Задача.
В 
 ,
,
 ,
,
 .
Найти
.
Найти  .
.
Решение.


По теореме косинусов:






 ,
,




Ответ:
 .
.
Можем подвести итоги урока.
Сегодня мы говорили об угле между двумя векторами. И выяснили, что он в отличии от угла между прямыми может быть и тупым. Но изменяется такой угол в пределах от 0 до 180°.
Причем величина угла не зависит от выбора точки, от которой будут отложены векторы.
Среди частных случаев мы выделили угол между сонаправленными векторами. Он равен нулю.
Так же нулю равен угол между векторами, если хотя бы один из них является нулевым вектором.
Ещё мы отметили, что угол между противоположно направленными векторами равен 180°.
Если же угол между векторами равен 90°, то такие векторы называют перпендикулярными.
Все эти сведения помогли нам успешно справиться с решением задач.

 Получите свидетельство
Получите свидетельство Вход
Вход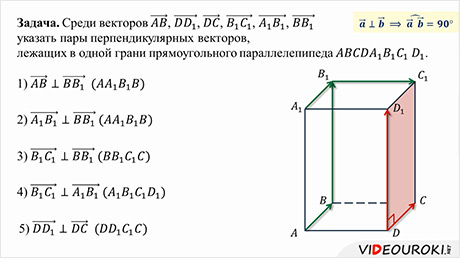



 0
0 5123
5123