Скалярное произведение векторов

Для начала вспомним, какие действия над векторами вам известны.

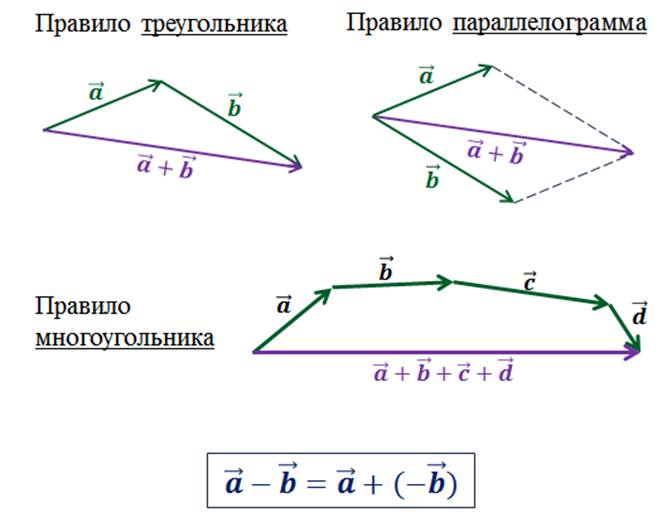
Итак, это сложение двух векторов по правилу треугольника или параллелограмма и нескольких векторов по правилу многоугольника. Вектор разности векторов  мы получали как вектор суммы векторов .

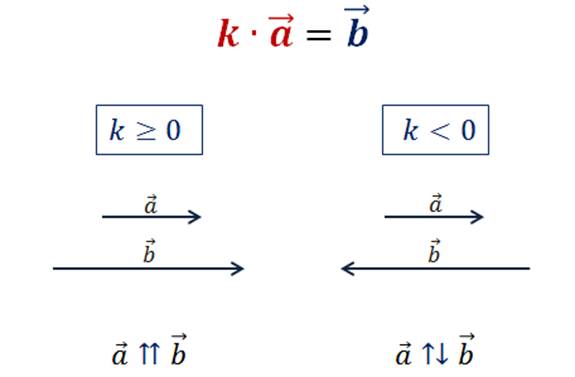
Также вам знакомо правило умножение вектора на число.

Сегодня вы познакомитесь с ещё одним действием над векторами — скалярным умножением векторов.

Определение. Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними.

Скалярное произведение векторов  обозначают так .

Или возможна запись без знака умножения.

Оно равно произведению длин данных векторов на косинус угла между ними.

Стоит вспомнить, что угол между векторами получают, откладывая данные векторы от одной точки. При этом выбирают угол меньший 180°

Обратите внимание, ранее, при выполнении сложения, вычитания векторов и умножения вектора на число, результатом каждого из этих действий мы получали некоторый вектор.

Результатом же скалярного произведения векторов является число.

Сейчас подробнее рассмотрим случай, когда скалярное произведение векторов равно 0.

Понятно, что для этого хотя бы один из множителей должен быть равен нулю.

Такими будут случаи, когда хотя бы один из векторов в произведении является нулевым.

Если же векторы  ненулевые, то косинус угла между ними должен быть равен 0.

Среди возможных значений градусной меры угла между двумя векторами только лишь косинус угла в 90° равен 0.

Отсюда получаем, что векторы  перпендикулярны.

Подытожим. Скалярное произведение равно нулю, если хотя бы один из векторов сомножителей является нулевым.

Ну, а скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.

Из формулы скалярного произведения также можно заметить, что, если векторы  не нулевые, то их длины всегда больше нуля, поэтому их произведение тоже положительно. А вот значение косинуса угла между ними может принимать как положительные, так и отрицательные значения.

Можно сказать, что скалярное произведение двух ненулевых векторов больше нуля, если угол между векторами острый. Равно нулю, если угол между ним прямой. И меньше нуля, если угол между данными векторами тупой. Ещё раз обратим внимание на то, что эти заключения верны для ненулевых векторов .

Задача. Найти скалярное произведение векторов  и , пользуясь данными рисунков.

Решение.

а)

б)

в)

г)

Мы рассмотрели примеры применения формулы скалярного произведения двух векторов и убедились, что скалярное произведение ненулевых векторов больше нуля, если угол между ними является острым, равно нулю — если векторы перпендикулярны, и меньше нуля — если угол между векторами тупой.

А сейчас рассмотрим сонаправленные векторы  и . Запишем формулу их скалярного произведения.

Вы должны помнить с прошлых уроков, что угол между сонаправленными векторами равен нулю. А косинус угла в 0° равен 1. Тогда получаем, что скалярное произведение сонаправленных векторов равно произведению их длин.

Говоря о противоположно направленных векторах, можно вспомнить, что угол между ними равен 180°. Значит, косинус равен -1.

Тогда скалярное произведение противоположно направленных векторов равно .

Что касается, скалярного произведения вектора на самого себя, то его называют скалярным квадратом вектора. Этот случай можно рассматривать в контексте сонаправленных векторов. Действительно, ведь векторы равны, а значит, и сонаправлены. Такое произведение равно произведению длин данного вектора.

Тогда получаем, что скалярный квадрат вектора равен квадрату его длины.

Задача. Найдём скалярные квадраты векторов , ,  и .

Решение.

Скалярное произведение векторов применяется не только в математике. Например, из курса механики известно, что работа постоянной силы F при перемещении из точки М в точку Н равна .

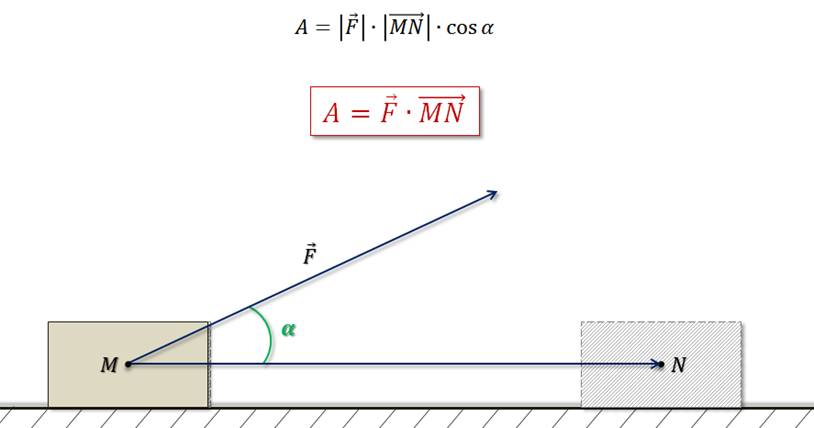
Тем самым получаем, что работа силы F равна скалярному произведению вектора силы  и вектора перемещения .

Вернёмся к скалярному произведению в математике и решим несколько задач.

Задача. К одной и той же точке приложены  и , действующие под углом в  друг к другу. , . Найти величину равнодействующей силы .

Решение.

1 способ

,

2 способ

,

Ответ: .

Задача. В ,где , проведена высота . Вычислить , , , .

Решение

, так как

Подведём итоги нашего урока.

Сегодня вы познакомились с новым действием над векторами — скалярным умножением векторов.

Скалярным произведением двух векторов называют произведение длин данных векторов на косинус угла между ними.

Проанализировав эту формулу, мы заметили, что скалярное произведение равно нулю, если хотя бы один из векторов сомножителей является нулевым. Ну, а скалярное произведение ненулевых векторов рано нулю, тогда и только тогда, когда данные векторы перпендикулярны.

Также, пользуясь знаниями об углах между сонаправленными и противоположно направленными векторами, мы выяснили, что скалярное произведение сонаправленных векторов равно произведению их длин, а скалярное произведение противоположно направленных векторов противоположно произведению их длин.

Введя понятия скалярного квадрата вектора, мы получили, что он равен квадрату длины данного вектора.

Знания о скалярном произведении векторов можно применять не только на уроках математики. Так же они широко используются в физике.