Материал урока.
С пирамидой мы с вами знакомились в курсе геометрии базовой школы. Давайте вспомним, какой многогранник мы назвали пирамидой и основные элементы пирамиды.
Итак, рассмотрим многоугольник A1A2…An и точку P, не лежащую в плоскости этого многоугольника. Соединим точку ПЭ отрезками с вершинами многоугольника. В итоге получим n треугольников: PA1A2, PA2A3, …, PAnA1. Многогранник, составленный из n-угольника A1A2…An и этих n треугольников, называется пирамидой.
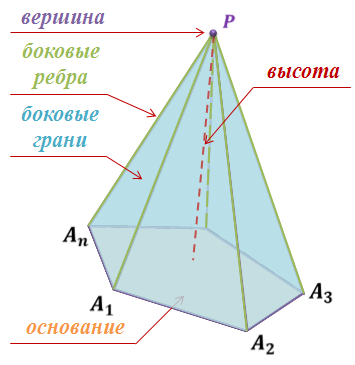
Многоугольник A1A2…An называется основанием пирамиды. Треугольники PA1A2, PA2A3, …, PAnA1 называются боковыми гранями пирамиды. Точка P – вершиной пирамиды, а отрезки PA1, PA2,…, PAn – ее боковыми ребрами.
Пирамиду с вершиной P и основанием A1A2…An называют n-угольной пирамидой и обозначают так: PA1A2…An.
Отрезок, соединяющий вершину пирамиды с плоскостью ее основания и перпендикулярный к этой плоскости, называется высотой пирамиды.
Объединение боковых граней называется боковой поверхностью пирамиды, а объединение всех граней называется полной поверхностью пирамиды. Тогда площадью боковой поверхности пирамиды называется сумма площадей ее боковых граней. А площадью полной поверхности пирамиды называется сумма площадей всех ее граней.
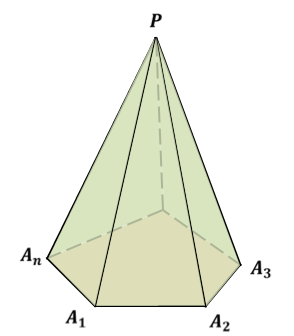
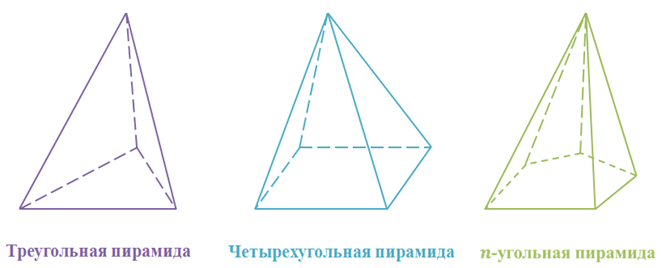
Пирамида в зависимости от того какой многоугольник лежит в основании имеет свое название. Если в основании лежит треугольник, то пирамида называется треугольной. Если четырехугольник – то четырехугольной пирамидой. А если n-угольник, то n-угольной пирамидой.
Решим задачу.
Задача. Основанием
пирамиды является ромб, сторона которого равна 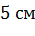 , а одна из
диагоналей равна
, а одна из
диагоналей равна 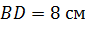 . Найти длину
боковых ребер пирамиды, если высота пирамиды проходит через точку пересечения
диагоналей основания и равна
. Найти длину
боковых ребер пирамиды, если высота пирамиды проходит через точку пересечения
диагоналей основания и равна 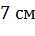 .
.
Решение.
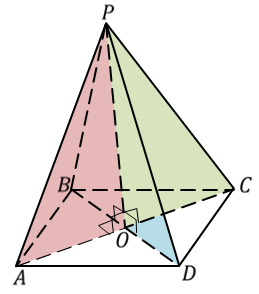
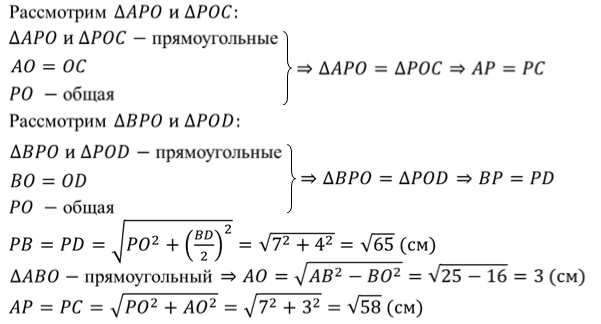
Ответ. 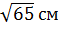 ,
, 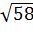 см.
см.
Давайте дадим определение правильной пирамиды.
Пирамида называется правильной, если ее основание – правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой. Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой.
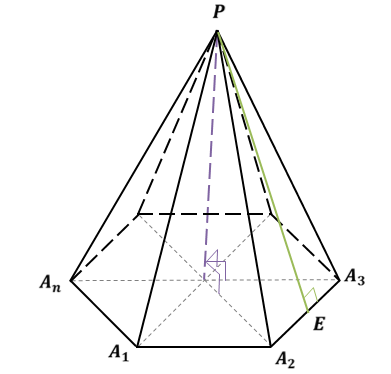
На сегодняшнем уроке мы подробно рассмотрим правильные пирамиды.
Сейчас давайте попробуем доказать одно из свойств правильной пирамиды. А именно докажем, что все боковые ребра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками.
Рассмотрим правильную пирамиду PA1A2…An. Сначала докажем, что все боковые ребра этой пирамиды равны. Проведем высоту пирамиды.
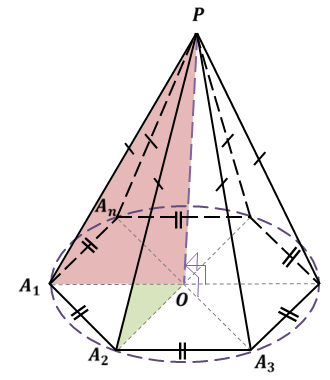
Поскольку основанием правильной пирамиды является правильный многоугольник, значит, вокруг основания правильной пирамиды можно описать окружность. Тогда каждое боковое ребро пирамиды есть ничто иное, как гипотенуза прямоугольного треугольника, одним катетом которого служит высота PO пирамиды, а другим – радиус описанной около основания окружности. Например, если рассмотреть треугольник OPA1, то OP равно h, OA1 равно R.
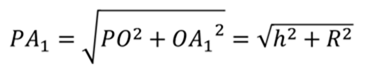
Таким образом, мы доказали, что боковые ребра правильной пирамиды равны. А значит, боковые грани правильной пирамиды – это равнобедренные треугольники. Поскольку в основании лежит правильный многоугольник, значит, основания боковых граней равны между собой. То есть боковые грани равны между собой по трем сторонам.
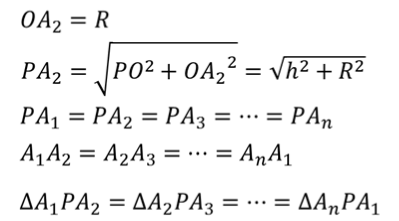
Что и требовалось доказать.
Теперь давайте сформулируем и докажем теорему о площади боковой поверхности правильной пирамиды.
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Доказательство.
Запишем формулу для вычисления площади боковой поверхности правильной пирамиды.
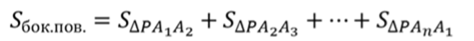
Мы уже доказали,
что боковые грани правильной пирамиды – равные равнобедренные треугольники.
Высоты этих треугольников равны апофеме пирамиды. Тогда площадь боковой грани
находится по формуле 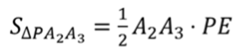 .
.
Подставим эти площади в формулу площади боковой поверхности. Вынесем половину апофемы за скобки, тогда в скобках получим периметр основания.
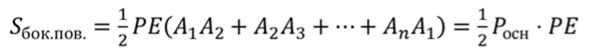
Что и требовалось доказать.
Решим несколько задач.
Задача. Радиус
окружности, вписанной в основание правильной четырехугольной пирамиды, равен 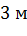 , высота
пирамиды равна
, высота
пирамиды равна 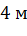 . Найти
площадь боковой поверхности пирамиды.
. Найти
площадь боковой поверхности пирамиды.
Решение.
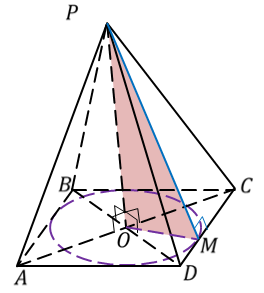

Ответ. 60 м2
Решим еще одну задачу.
Задача. Радиус
окружности, описанной около основания правильной треугольной пирамиды, равен 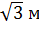 .
. 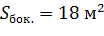 . Найти длину
апофемы.
. Найти длину
апофемы.
Решение.
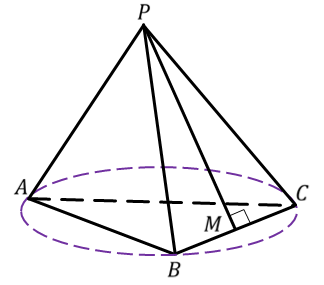
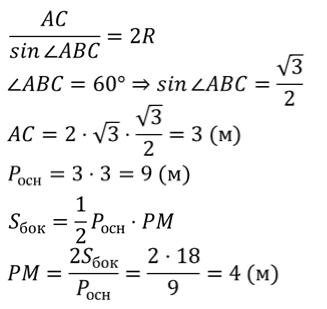
Ответ. 4 м
Подведем итоги урока.
Сегодня на уроке мы вспомнили, какая фигура называется пирамидой. Какие пирамиды называются правильными. Познакомились со свойствами правильных пирамид. Решили несколько задач.

 Получите свидетельство
Получите свидетельство Вход
Вход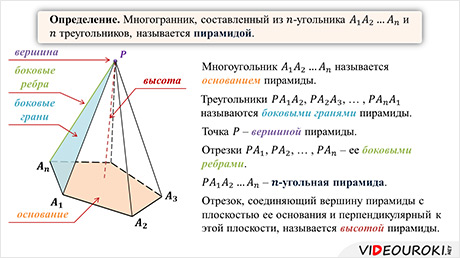



 1
1 20363
20363








Спасибо, огромное. Вы очень нас выручили.