Материал урока.
На прошлых уроках мы работали с пирамидами. Давайте вспомним, какой многогранник называется пирамидой, что такое правильная пирамида, вспомним свойства правильной пирамиды.
Многогранник, составленный из -угольника  и
и  треугольников, называется пирамидой.
треугольников, называется пирамидой.
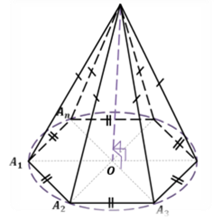
Пирамида называется правильной, если ее основание – правильный многоугольник.
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
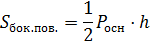
Все боковые ребра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками.
Пусть нам дана пирамида PA1A2…An. Проведем секущую плоскость β, параллельную плоскости основания пирамиды и пусть эта плоскость пересекает боковые ребра в точках B1,B2,…, Bn.
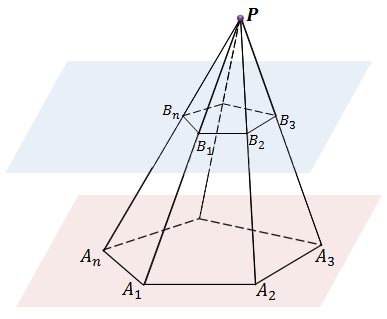
Плоскость β разбивает пирамиду на две фигуры: пирамиду PB1B2…Bn и многогранник. Многогранник, гранями которого являются n-угольники A1A2…An и B1B2…Bn, расположенные в параллельных плоскостях и n четырехугольников A1A2B2B1, A2A3B3B2,…, AnA1B1Bn называется усеченной пирамидой.
Вокруг нас много примеров усеченных пирамид. Вытяжка над кухонной плитой имеет форму усеченной пирамиды.клавиши клавиатуры и другие предметы.
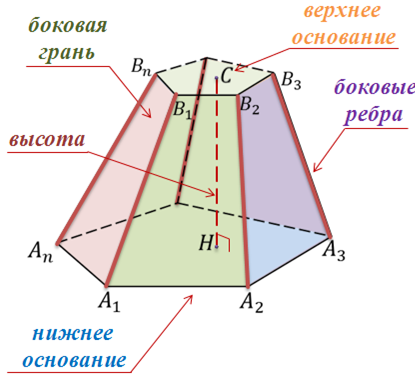
N-угольники A1A2…An и B1B2…Bn называются соответственно верхним и нижним основанием. Четырехугольники A1A2B2B1, A2A3B3B2,…, AnA1B1Bn называются боковыми гранями.
Отрезки A1B1,…, AnBn называются боковыми рёбрами усеченной пирамиды.
Усеченную пирамиду обозначают так A1A2…AnB1B2…Bn. Возьмем на верхнем основании произвольную точку C и из этой точки опустим перпендикуляр на нижнее основание. Этот перпендикуляр называется высотой усеченной пирамиды.
Теперь давайте докажем, что боковые грани усеченной пирамиды – это трапеции.
Для доказательства рассмотрим грань A1A2B2B1. Понятно, что для других боковых граней доказательство будет проводится аналогично.
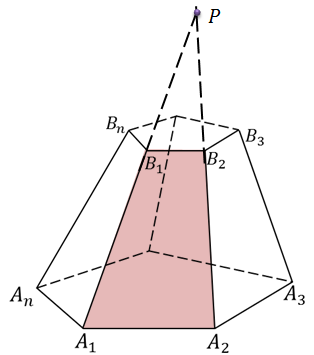
Поскольку секущая плоскость проводилась параллельно плоскости основания, то можно записать, что A1A2 параллельно B1B2. Очевидно, что две другие стороны четырехугольника A1A2B2B1 не параллельны (они пересекаются в точке P). Получаем, что этот четырехугольник – трапеция. Очевидно, что все остальные боковые грани тоже будут трапециями.
Как и в случае с пирамидой, усеченная пирамида тоже может быть правильной.
Усеченная пирамида называется правильной, если она получена сечением правильной пирамиды плоскостью, параллельной основанию.
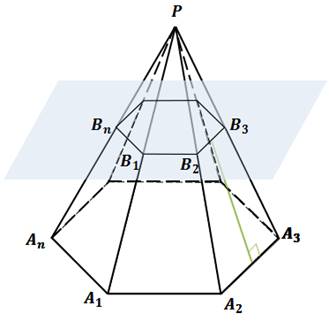
Основаниями усеченной пирамиды являются правильные многоугольники, а боковые грани – равнобедренные трапеции.
Высоты этих трапеций называются апофемами.
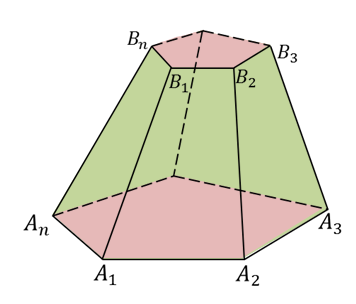
Объединение боковых граней называется боковой поверхностью усеченной пирамиды, а объединение всех граней называется полной поверхностью усеченной пирамиды. Тогда площадью боковой поверхности пирамиды называется сумма площадей ее боковых граней.
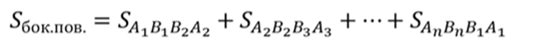
А площадью полной поверхности пирамиды называется сумма площадей всех ее граней.
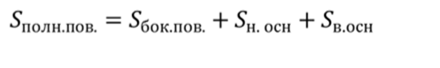
Теперь давайте сформулируем и докажем теорему о площади боковой поверхности правильной усеченной пирамиды.
Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров основания на апофему.
Доказательство.
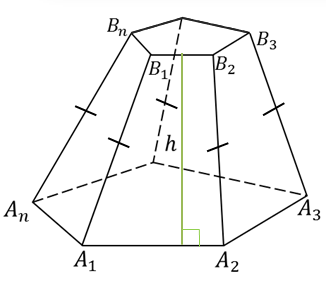
Запишем формулу для нахождения площади боковой поверхности усеченной пирамиды.
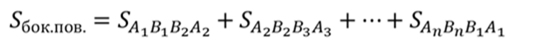
Поскольку усеченная пирамида правильная, значит, ее гранями будут равнобедренные трапеции.
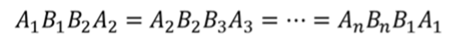
Площадь равнобедренной трапеции равна произведению полусуммы оснований на высоту. Высота боковой грани есть ничто иное как апофема усеченной пирамиды.
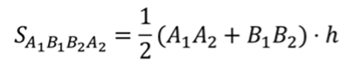
Подставим все в исходную формулу, вынесем половину апофемы за скобки, а в скобках сгруппируем стороны по основаниям. Тогда получим, что площадь боковой поверхности будет равна произведению полусуммы периметров оснований усеченной пирамиды на апофему.
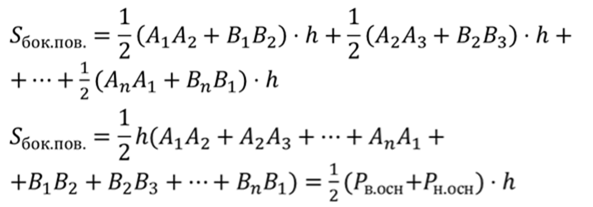
Что и требовалось доказать.
Решим несколько задач.
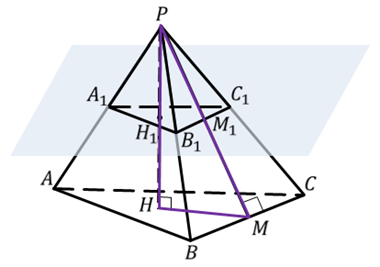
Задача. Стороны
оснований правильной усеченной четырехугольной пирамиды 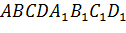 равны
равны 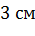 и
и  . Высота пирамиды
равна
. Высота пирамиды
равна 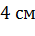 . Найти площадь
боковой поверхности.
. Найти площадь
боковой поверхности.
Решение.
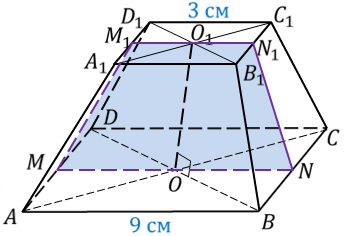
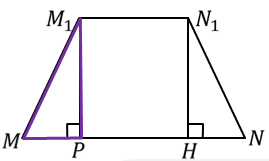
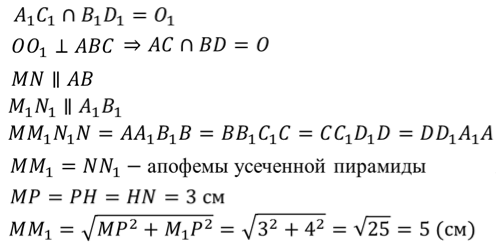
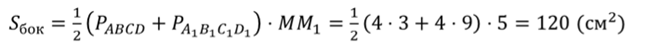
Ответ. 120 см2
Решим еще одну задачу.
Задача. Пирамида пересечена плоскостью, параллельной основанию. Доказать что боковые ребра и высота пирамиды делятся этой плоскостью на пропорциональные части.
Решение.
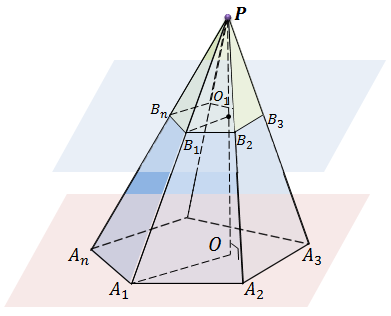
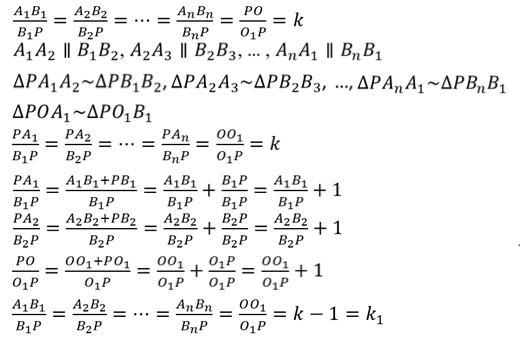
Что и требовалось доказать.
Решим еще одну задачу.
Задача. Правильная
треугольная пирамида 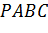 с высотой
с высотой  и стороной основания
равной
и стороной основания
равной 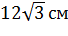 рассечена плоскостью
рассечена плоскостью
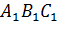 , проходящей через
середину
, проходящей через
середину 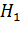 высоты
высоты 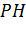 параллельно
основанию
параллельно
основанию 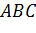 . Найти площадь
боковой поверхности полученной усеченной пирамиды.
. Найти площадь
боковой поверхности полученной усеченной пирамиды.
Решение.
 Ответ.
135
Ответ.
135 см2.
см2.
Подведем итоги урока. Сегодня на уроке мы познакомились с такими понятиями как усеченная пирамида, правильная усеченная пирамида. Рассмотрели свойства правильной усеченной пирамиды. Решили несколько задач.

 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 22383
22383

