Материал урока.
Мы уже знакомились с призмами. Сегодня мы повторим основные понятия, которые связаны с ними.
Давайте вспомним, какой многогранник мы назвали призмой.
Рассмотрим два равных многоугольника A1A2…An и B1B2…Bn, расположенные в параллельных плоскостях. Причем расположены эти многоугольники так, чтобы равные стороны этих многоугольников, т.е. A1A2 и B1B2, A2A3 и B2B3 … AnA1 и BnB1, были параллельными.
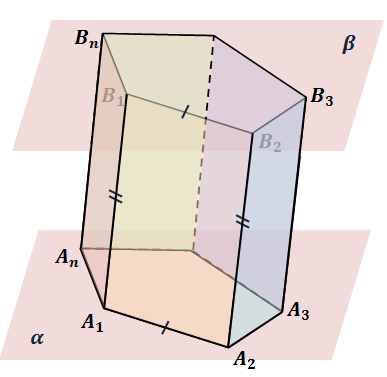
Теперь проведем отрезки A1B1, A2B2, A3B3…AnBn. В итоге, получим n четырехугольников A1B1B2A2, A2B2B3A3…AnBnB1A1.
Указанные четырехугольники являются параллелограммами. Рассмотрим например, четырехугольник A1B1B2A2. Его противоположные стороны A1A2 и B1B2 равны и параллельны по построению. Следовательно, и стороны A1B1 и A2B2 тоже равны и параллельны. Напомню, что четырёхугольник, у которого противоположные стороны попарно параллельны, называется параллелограммом. Значит, рассматриваемый нами четырехугольник A1B1B2A2 – параллелограмм.
Построенный многогранник A1A2…AnB1B2…Bn, называется n-угольной призмой.
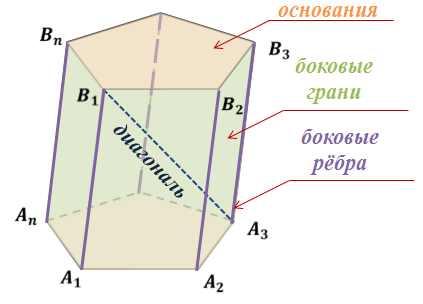
Равные n-угольники называются основаниями призмы. Параллелограммы – боковыми гранями призмы. А стороны боковых граней, не являющиеся сторонами оснований призмы, называются боковыми ребрами призмы.
На рисунке, A1A2…AnB1B2…Bn – n-угольная призма. А1A2…An и B1B2…Bn – основания призмы, параллелограммы A1A2B2B1,…, AnA1B1Bn– боковые грани. А стороны A1B1,…, AnBn – боковые ребра призмы. Все они равны и параллельны друг другу, как стороны параллелограммов.
Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани, например, B1A3, называется диагональю призмы.
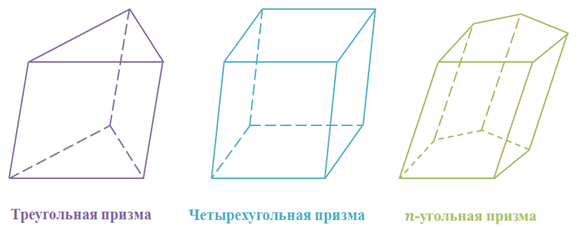
Призма в зависимости от того какой многоугольник лежит в основании имеет свое название. Если в основании лежит треугольник, то призма называется треугольной. Если четырехугольник – то четырехугольной призмой. А если n-угольник, то n-угольной призмой.
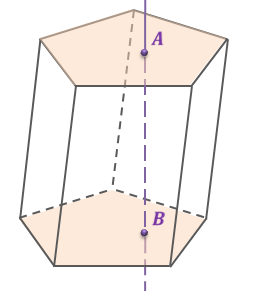
Теперь узнаем, что называют высотой призмы. Выберем произвольную точку А одного из оснований и проведем через нее прямую, перпендикулярную к плоскости другого основания и пересекающую ее в точке B. Отрезок, AB называется высотой призмы.
В зависимости от того перпендикулярны ли ребра основанию, призмы можно подразделить на прямые и наклонные.
Если все боковые ребра призмы перпендикулярны к плоскостям ее оснований, то призма называется прямой. Если же боковые ребра не перпендикулярны основанию, то призма называется наклонной. На рисунке изображены примеры прямой и наклонной призм.

Обратите внимание, у прямой призмы боковые грани являются прямоугольниками, а у наклонной призмы – параллелограммы.
Прямая призма, основаниями которой являются правильные многоугольники, называется правильной.
Объединение боковых граней называется боковой поверхностью призмы, а объединение всех граней называется полной поверхностью призмы. Тогда площадью боковой поверхности призмы называется сумма площадей ее боковых граней.
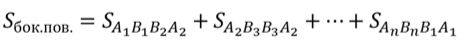
А площадью полной поверхности призмы называется сумма площадей всех ее граней.
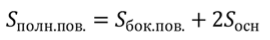
Это все нам известно с курса геометрии базовой школы.
Сегодня мы выведем новую формулу для вычисления площади боковой поверхности прямой призмы.
Сформулируем и докажем теорему. Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.
Доказательство.
Выше мы уже вспоминали, что все боковые грани прямой призмы – прямоугольники. Основания этих прямоугольников – стороны основания призмы. А высоты этих прямоугольников равны высоте призмы. Мы знаем, что площадь боковой поверхности призмы равна сумме площадей каждой из боковых граней, то есть в случае прямой призмы это будет сумма произведений сторон основания на высоту призмы.
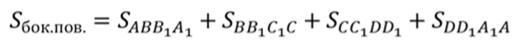
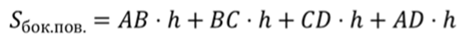
Вынесем множитель р за скобки, тогда в скобках получим сумму сторон основания призмы, другими словами – в скобках мы получим периметр основания.
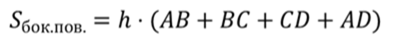
Тогда можно записать, что площадь боковой поверхности прямой призмы равна произведению высоты на периметр основания.

Решим несколько задач.
Задача. Основанием прямой призмы является равнобедренная
трапеция с основаниями, которые равны 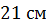 и
и 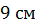 .
Высота призмы равна
.
Высота призмы равна 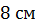 .
Найти площадь боковой поверхности, если боковое ребро равно
.
Найти площадь боковой поверхности, если боковое ребро равно 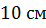 .
.
Решение.
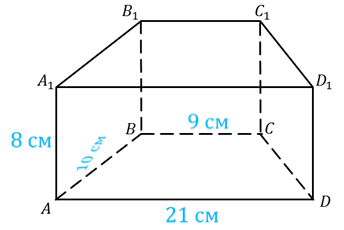
Поскольку призма прямая, то воспользуемся только что доказанной формулой.
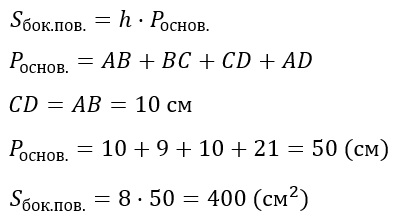
Ответ. 400 см2.
Решим еще одну задачу.
Задача. В правильной треугольной призме сторона основания
равна 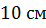 , а
высота призмы равна
, а
высота призмы равна 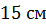 .
Вычислить площадь боковой и полной поверхности призмы.
.
Вычислить площадь боковой и полной поверхности призмы.
Решение.
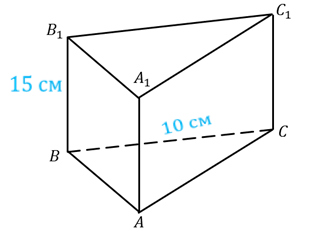
Поскольку по условию призма правильная, значит, она прямая. Применим только что доказанную формулу.
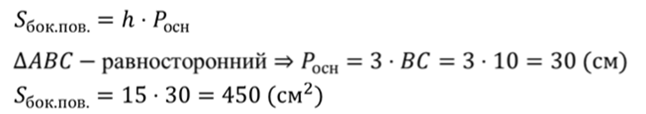 Запишем формулу для вычисления площади полной
поверхности призмы.
Запишем формулу для вычисления площади полной
поверхности призмы.
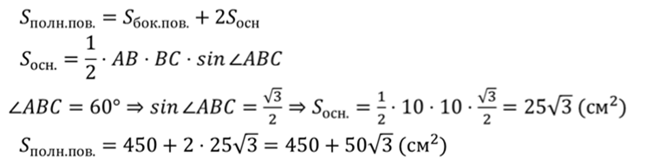
Ответ. 450 см2,
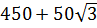 см2
см2
Решим еще одну задачу.
Задача. Доказать, что площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на боковое ребро.
Доказательство.
В качестве примера, мы возьмем треугольную призму, для других призм это утверждение доказывается аналогично.
Перпендикулярным сечением называется пересечение призмы и плоскости, перпендикулярной ее боковому ребру.
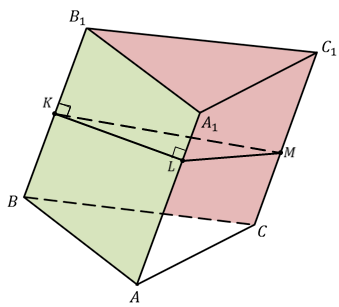
Для построения перпендикулярного сечения выберем, например, на ребре BB1 произвольно точку К. В плоскости грани AA1B1B через точку К проведем прямую KL перпендикулярную к ребру BB1. Эта прямая будет перпендикулярна к ребру AA1, поскольку ребра AA1 и BB1 параллельны.
Теперь через точку К в плоскости грани BB1C1C проведем прямую КМ перпендикулярную ребру BB1. Тогда из того, что BB1 перпендикулярно пересекающимся прямым KL и КМ плоскости KLM следует, что BB1 перпендикулярно плоскости KLM.
То есть построенное сечение KLM перпендикулярно боковому ребру. А значит, это и есть перпендикулярное сечение призмы.
Тогда надо доказать, что площадь боковой поверхности призмы равна произведению периметру треугольника KLM и бокового ребра BB1.
Любая боковая грань призмы – это параллелограмм. Рассмотрим грань ABB1A1. КL – это высота параллелограмма ABB1A1. Поэтому для нахождения площади этой грани можно применить формулу:
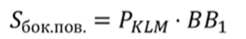
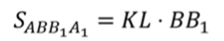
В качестве основания мы берем сторону BB1, так как высота проводилась к этой стороне.
Аналогично можно записать:
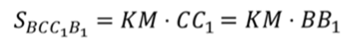
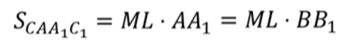
Запишем формулу для вычисления площади боковой поверхности. Заменим площадь каждой грани полученной формулой.
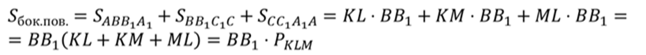
Решим еще одну задачу.
Задача. Боковое ребро наклонной четырехугольной призмы равно 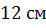 . Перпендикулярным сечением является ромб со стороной
. Перпендикулярным сечением является ромб со стороной 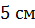 . Найти площадь боковой поверхности.
. Найти площадь боковой поверхности.
Решение.
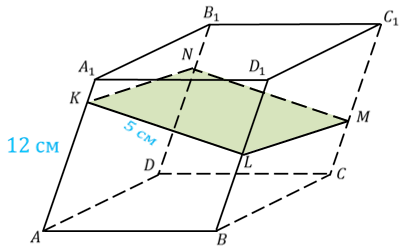
Воспользуемся только что доказанным утверждением.
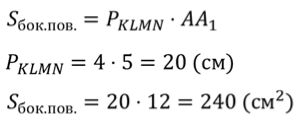
Решим еще одну задачу.
Задача. Основанием прямой призмы является равнобедренная
трапеция с основаниями 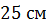 ,
, 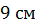 и высотой
и высотой 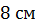 .
Найти двугранные углы при боковых ребрах призмы.
.
Найти двугранные углы при боковых ребрах призмы.
Решение.
Для определения двугранных углов, нам необходимо найти соответствующие линейные углы.
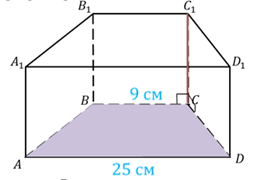
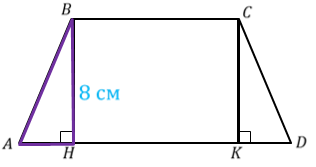

Ответ. 45°, 135°.
Подведем итоги урока.
Сегодня на уроке мы вспомнили, какая фигура называется призмой, основные элементы призмы. Виды призм. Вывели формулы для вычисления площади боковой поверхности прямой и наклонных призм. Решили несколько конкретных задач.

 Получите свидетельство
Получите свидетельство Вход
Вход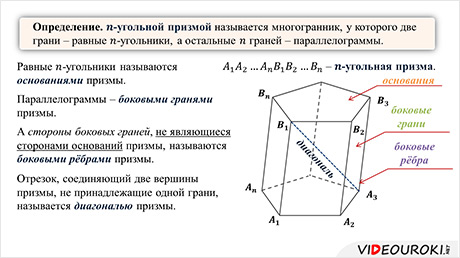



 0
0 9699
9699