Найдём
связь между графиками функций 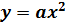 и
и
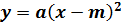 .
.
Для
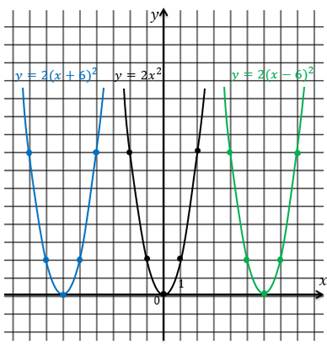
этого изобразим в одной координатной плоскости графики функций 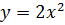 ,
,
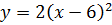 ,
,
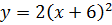 .
.
Составим таблицы значений для функций:
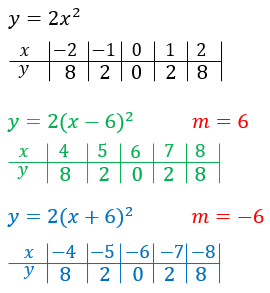
Видно,
что график функции 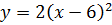 можно
получить из графика
можно
получить из графика 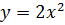 в
квадрате параллельным переносом относительно оси х вправо на 6 единиц, m=6.
А график функции
в
квадрате параллельным переносом относительно оси х вправо на 6 единиц, m=6.
А график функции 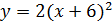 параллельным
переносом влево на 6 единиц, m=-6.
параллельным
переносом влево на 6 единиц, m=-6.
Определение:
График
функции 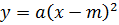 является
параболой, которую можно получить из
графика функции
является
параболой, которую можно получить из
графика функции 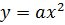 с
помощью параллельного переноса вдоль оси х на m единиц
вправо, если m>0,
и на -m
единиц
влево, если m<0.
с
помощью параллельного переноса вдоль оси х на m единиц
вправо, если m>0,
и на -m
единиц
влево, если m<0.
Пример.
Изобразить
графики функций вида  ,
пользуясь уже известными определениями.
,
пользуясь уже известными определениями.
Используя
шаблон  ,
изобразим графики функции
,
изобразим графики функции  .
.
Сначала рассмотрим шаблон. Не трудно составить таблицу значений этой функции:

Получаем параболу.
Взглянем
на формулу, которой задана функция  .
Это функция вида
.
Это функция вида 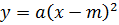 ,
в данном случае m=-4.
Получить график этой функции можно с помощью параллельного переноса параболы
,
в данном случае m=-4.
Получить график этой функции можно с помощью параллельного переноса параболы  относительно
оси х на 4 единицы влево.
относительно
оси х на 4 единицы влево.

Получили
график функции  .
Вершина данной параболы имеет координаты (-4,0).
.
Вершина данной параболы имеет координаты (-4,0).
Заметим,
что вершина параболы 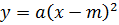 будет
иметь координаты (m,0).
будет
иметь координаты (m,0).
Определение:
Функция
вида  – это парабола, которую можно
получить из графика функции
– это парабола, которую можно
получить из графика функции  в
квадрате с помощью двух параллельных переносов:
в
квадрате с помощью двух параллельных переносов:
1. вдоль оси y на n единиц вверх, если n>0, и на -n единиц вниз, если n<0;
2. вдоль оси x на m единиц вправо, если m>0, и на -m единиц влево, если m<0.
Параллельные переносы можно производить в любом порядке.
Вершина этой параболы будет иметь координаты (m,n).
Пример.
С
помощью шаблона параболы  изобразить
график функции
изобразить
график функции  .
.
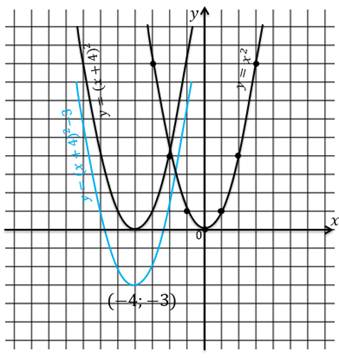
На
рисунке видно, что m=-4,
сдвигаем точки шаблона на 4 единицы влево и n=-3,
сдвигаем полученный график на 3 единицы вниз. Получили график функции  .
Вершина имеет координаты (-4,-3).
.
Вершина имеет координаты (-4,-3).

 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 34555
34555

