Построение графика квадратичной функции

Графиком любой квадратичной функции является парабола. У каждой параболы есть вершина, при изображении графика важно знать её координаты. Вершина параболы 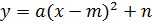 имеет координаты (m,n).

Определите координаты вершин для парабол:

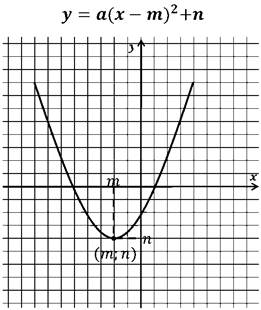
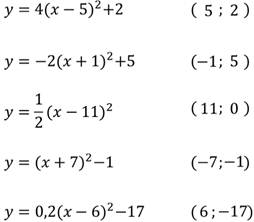
Определим координаты вершины параболы, которая является графиком квадратичной функции записанной в виде .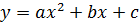

Преобразуем квадратный трёхчлен, выделим из него квадрат двучлена:

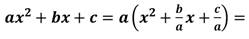
Второе слагаемое представим в виде удвоенного произведения:

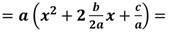
Выделим квадрат суммы:

После сокращения получаем:

Отсюда запишем, что:

Вывод.

Графиком функции 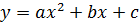 является парабола, которую можно получить из параболы с помощью двух параллельных переносов: сдвига относительно оси x и сдвига относительно оси y. Данная парабола имеет вершину с координатами (m,n), где , . Осью симметрии является прямая x=m.

Пример.

Найти координаты вершины параболы .

Вершина будет иметь координаты (m,n), каждую из которых можно получить по формуле. Подставим коэффициенты квадратичной функции в формулу и найдём эти значения:

Вершина параболы имеет координаты (-2,-5).

Воспользуемся наиболее простым способом: сначала найдём m вершины по формуле. И учитывая, что вершина принадлежит графику функции, подставим m вместо аргумента в функцию:

Получили вершину, которая имеет координаты (-2,-5).

Алгоритм построения графика квадратичной функции:

1.     Определить направление ветвей парабола. Если a>0, то ветви направлены вверх, если a<0, то — вниз.

2.     Найти координаты вершины параболы и отметить её на координатной плоскости. Применив формулу , найдём абсциссу вершины параболы, и, подставив это значение в формулу, задающую функцию, найдем ординату этой точки.

3.     Определить ось симметрии x=m.

4.     Построить ещё несколько точек принадлежащих параболе, составив таблицу значений функции с учётом оси симметрии.

5.     Соединить отмеченные точки плавной линией.

Пример.

Изобразить график функции .

1.                Определим направление ветвей параболы:

2.                Найдём координаты вершины:

Получили вершину с координатами (-2, -3).

3.                Определим ось симметрии:

4.                Составим таблицу значений:

Выбранные значения симметричны относительно оси симметрии.

5.                Отметим и соединим полученные точки на координатной плоскости:

Получили параболу, которая является графиком функции.

Пример.

Изобразить график функции  и описать её свойства.

Изобразим график функции:

1.                Определим направление ветвей параболы:

2.                Найдём координаты вершины параболы:

Вершина имеет координаты (-2,-4).

3.                Определим ось симметрии:

4.                Составим таблицу значения функции:

5.                Соединив эти точки, получаем:

Определим свойства функции.

Областью определения и областью значений являются:

Определим нули функции:

Перечислим промежутки знакопостоянства функции:

Опишем промежутки монотонности: