Функция y=x^n

Определение:

Функцию, заданную формулой , называют степенной функцией с натуральным показателем, где x - независимая переменная, а n - натуральное число.

Например:

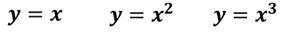
Существуют два случая степенной функции: с чётным показателем и с нечётным показателем.

Рассмотрим пример: найти на рисунке степенные функции с чётным показателем и с нечётным показателем.

С чётным показателем:

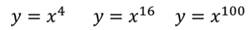
С нечётным показателем:

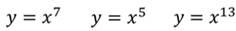
Определение:

Областью определения любой степенной функции с натуральным показателем является множество всех действительных чисел.

Рассмотрим случай, когда n - чётное число. График выглядит так:

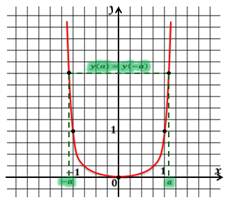
Опишем свойства этой функции:

1.     Если x=0, то y=0.

2.     Если x≠0, то y>0, т.к. чётная степень как положительного, так и

отрицательного числа положительна.

3.     Противоположным значениям аргумента соответствуют равные значения функции.

4.     Функция возрастает и убывает на промежутке:

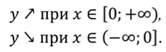
5.     При любых значения аргумента функция принимает неотрицательные значения. Областью значений является:

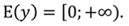
Рассмотрим случай, когда n - нечётное число (n>1).

График выглядит так:

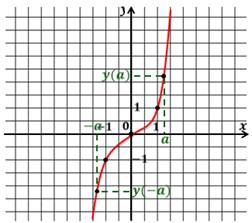
Опишем свойства этой функции:

1.     Если x=0, то y=0. Ноль в любой степени равен нулю.

Если x>0, то y>0.

Если x<0, то y<0.

2.     Нечётная степень отрицательного числа отрицательна.

3.     Противоположным значениям аргумента соответствуют противоположные значения функции.

4.     Функция возрастает на всей области определения, принимая любые значения.

5.     Областью значений является:

Рассмотрим пример: сравнить значения выражений:

Показатель степени у обоих выражений одинаковые. Рассмотрим график степенной функции с нечётным показателем:

На рисунке изображен график степенной функции с нечётным показателем, функция возрастает на всей области определения. В данном случае при любых значениях аргумента из множества всех действительных чисел, т.е. большему значению аргумента соответствует большее значение функции.

Рассмотрим пример: сравнить значения выражений:

Показатель степени у обоих выражений нечётный, т.е большему значению аргумента соответствует большее значение функции.

Рассмотрим пример: сравнить значения выражений:

Рассмотрим график:

Показатель степени у обоих выражений чётный, т.е. большему значению аргумента соответствует меньшее значение функции.

Пример.

Сравнить значения выражений:

Данные значения принадлежат промежутку возрастания, то есть большему значению аргумента соответствует большее значение функции.

Пример.

Определить, принадлежат ли графику функции  точки А(2,16), В(3,9), С(-1,1).

Точка А.

Значит, точка А принадлежит графику функции.

Точка Б.

Значит, точка Б не принадлежит графику функции.

Точка С.

Значит, точка С принадлежит графику функции.