Изобразим в одной координатной плоскости графики функций:

Составим таблицы значений для каждой функции:

Запомните.
График функции  является параболой, которую можно
получить из графика функции
является параболой, которую можно
получить из графика функции  с
помощью параллельного переноса вдоль оси у на n единиц
вверх, если n>0,
и на -n
единиц
вниз, если n<0.
с
помощью параллельного переноса вдоль оси у на n единиц
вверх, если n>0,
и на -n
единиц
вниз, если n<0.
Нам
известно, что график функции  ,
всегда проходит через точку начала координат, причём она является вершиной
параболы. Легко получить, что вершина параболы
,
всегда проходит через точку начала координат, причём она является вершиной
параболы. Легко получить, что вершина параболы  будет
иметь координаты (0, n).
Так как выполняется параллельный перенос относительно оси y вверх или вниз.
будет
иметь координаты (0, n).
Так как выполняется параллельный перенос относительно оси y вверх или вниз.
Рассмотрим
пример: изобразим график функции  ,
используя шаблон
,
используя шаблон  .
.

Составим таблицу значений:

Соединяем точки и получаем параболу:

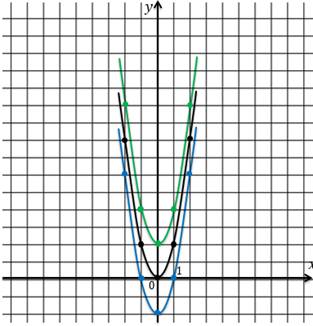
Перенесём ключевые точки графика на 3 единицы вниз, проведём через полученные точки параболу.
Используя
этот же шаблон, изобразим график функции  :
:
Составим таблицу значений:

Отобразим точки на графике.
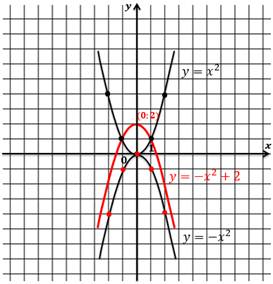
Для
функции  ,
отобразим возможные ключевые точки графика симметрично относительно оси х.
,
отобразим возможные ключевые точки графика симметрично относительно оси х.
С помощью параллельного переноса относительно оси у перенесем ключевые точки на 2 единицы вверх:

Получили
график функции  из
шаблона
из
шаблона  ,
с помощью осевой симметрии относительно оси х и параллельного переноса
относительно оси у на 2 единицы вверх. Вершина полученной параболы имеет
координаты (0,2).
,
с помощью осевой симметрии относительно оси х и параллельного переноса
относительно оси у на 2 единицы вверх. Вершина полученной параболы имеет
координаты (0,2).

 Получите свидетельство
Получите свидетельство Вход
Вход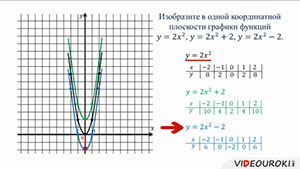



 4
4 12102
12102


Здравствуйте, Светлана. Нам важно мнение каждого клиента. Обязательно учтем Ваши замечания в будущем.
Тогда и нужно говорить: Значение игрек равно.
Здравствуйте, Светлана. Благодарим Вас за внимание к нашему проекту. Обратите внимание, в уроке комплекта, когда произносится фраза, что "икс\игрек равно и пр.", понимается в первую очередь "значение переменной икс\игрек". Отсюда такая форма.
При построении графиков звучит фраза:" Игрек равно."
Игрек и икс мужского рода. Игрек не равно, а игрек равен! Икс равен!
Учитель должен говорить грамотно, тем более на видео.