Функция y=ax^2, её график и свойства

Определение:

Квадратичной называют функцию вида:

Графиком квадратичной функции является парабола. Она состоит из двух ветвей и имеет вершину.

Ветви могут быть направлены вверх:

Ветви могут быть направлены вниз:

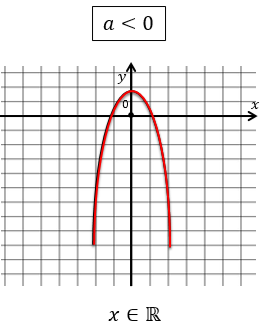
Квадратичная функция имеет свои свойства. Поговорим о них. В своей вершине квадратичная функция сменяет своё поведение с убывания на возрастание и с возрастания на убывание. Понятно, что областью определения в обоих случаях будет множество всех действительных чисел. Если говорим о нулях функции, то мы имеем ввиду те значения, при которых функция у=0. Когда находят нули функции по графику, то ищут точки пересечения графика с осью х. Если же находят нули функции по уравнению, то значение функции принимают равное 0. Тем самым получаем квадратное уравнение. Оно может иметь 2, 1 корень или не иметь корней. Соответственно, график может иметь 2 точки пересечения с осью х, 1 точку пересечения с осью х или не пересекать её. Понятно, что нулями квадратичной функции являются корни соответствующего квадратного уравнения. По графику удобно находить промежутки знакопостоянства и промежутки монотонности функции.

Пример: по графику квадратичной функции опишите её свойства.

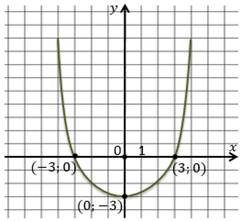
На рисунке изображена парабола, ветви которой направлены вверх, значит a>0. Опишем её свойства.

Областью определения и областью значений являются:

Нулями функции являются:

Промежутки знакопостоянства:

Промежутки монотонности:

Заметим, что описать свойства функции по её графику проще, чем по формуле. Поэтому очень важно уметь изображать график функции.

Рассмотрим частный случай квадратичной функции:

Изобразим график этой функции схематично и обратим внимание на некоторые её свойства. Возможны два случая изображения графика.

Областью определения в обоих случаях является:

Область значений:

Функция такого вида обращается в ноль только при х=0, график будет пересекать ось х в одной точке. Первым свойством мы запишем, что если:

Другими словами график такой функции всегда проходит через точку начала координат. Причём эта точка является вершиной параболы.

Если же

то график расположен выше или ниже оси Х.

Если взять противоположные значения аргумента, то видно, что им соответствуют одинаковые значения функции. Противоположным значениям аргумента соответствуют равные значения функции. Другими словами график функции симметричен относительно оси у.

Промежутки монотонности:

Заметим, что:

Пример.

В одной координатной плоскости изобразим графики функций:

Составим таблицу значений для первой функции.

Составим таблицу значений для второй функции

Получим два графика, они симметричны относительно оси х.

Рассмотрим пример: изобразим в одной координатной плоскости графики функции:

Составим таблицу значений для функции:

Составим таблицу значений для функции:

Составим таблицу значений для функции:

Изобразим графики этих функций:

График функции у=ах² можно получить из параболы у=х² растяжением от оси х в а раз, если а>0, и сжатием к оси х в 1/а раз к оси х, если 0<а<1.