Разложение квадратного трёхчлена на множители

Квадратный трёхчлен - это трёхчлен вида:

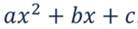
Чтобы найти корни квадратного трёхчлена, нужно решить квадратное уравнение:

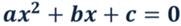
Разложим квадратный трёхчлен на множители, применяя известные способы разложения на множители: вынесение общего множителя за скобки, способ группировки, разложение многочлена на множители с помощью формул сокращённого умножения.

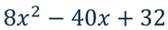
Вынесем общий множитель за скобки:

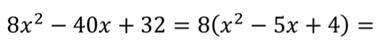
Воспользуемся способом группировки:

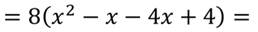
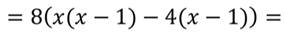
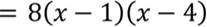
Видим, что в разложении квадратного трёхчлена на множители нет случайных чисел, первый множитель является старшим коэффициентом квадратного трёхчлена, а далее записано произведение разностей переменной и одного из корней квадратного трёхчлена.

Запишем квадратный трёхчлен в общем виде:

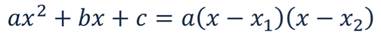
Первым множителем является старший коэффициент, вторым - разность переменной и первого корня уравнения, третьим - разность переменной и второго корня уравнения.

Если квадратный трёхчлен имеет один корень, это значит что их два, но они одинаковые, тогда при разложении получится:

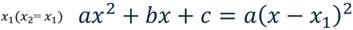
Если квадратный трёхчлен не имеет корней, то говорят, что его нельзя разложить на множители, являющиеся многочленами первой степени.

Выполним следующие задания:

1. Разложим на множители квадратный трёхчлен:

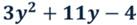
Найдём корни квадратного трёхчлена, решив соответствующее квадратное уравнение:

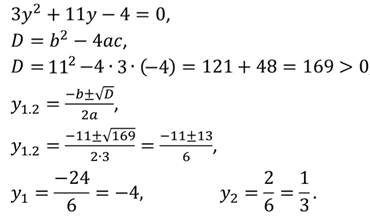
Получим выражение:

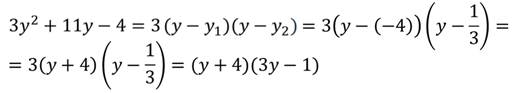
Разложим на множители ещё один квадратный трёхчлен:

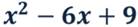
Найдём корни соответствующего квадратного уравнения:

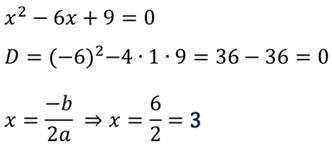
Получим:

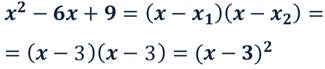
2. Сократите дробь:

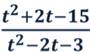
Разложим числитель на множители:

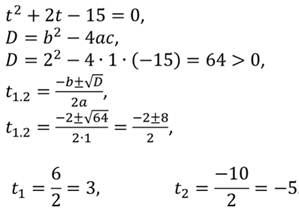
Разложим знаменатель на множители:

Получим:

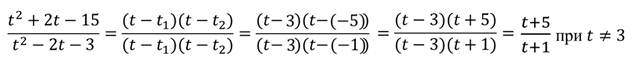
3.                Составьте квадратный трёхчлен, корнями которого являются числа 7 и -2.