Квадратный трёхчлен и его корни

Квадратный трёхчлен, это тот многочлен, который записан в левой части квадратного уравнения:

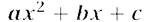
Коэффициенты квадратного трёхчлена имею такие же названия, как и коэффициенты квадратного уравнения:

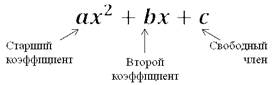
Найдите среди записанных многочленов те, которые являются квадратными трёхчленами:

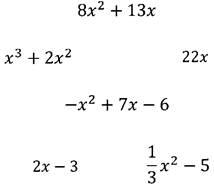
Получим:

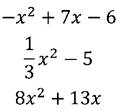
Определение:

Значение переменной, при котором многочлен равен нулю, называют корнем многочлена.

Найдём корни многочлена:

Для этого решим уравнение:

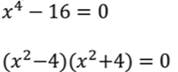
Левую часть уравнения можно разложить на множители с помощью формулы разности квадратов, получим:

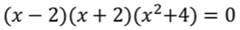
Произведение равно нулю, когда хотя бы один из множителей равен нулю, получаем:

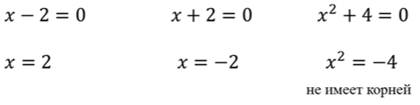
Ответ:

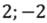
Вывод:

Чтобы найти корни квадратного трёхчлена

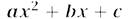
нужно решить квадратное уравнение

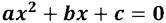
Найдите корни квадратных трёхчленов:

1.                Найдём корни первого квадратного трёхчлена

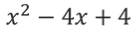
Решим квадратное уравнение:

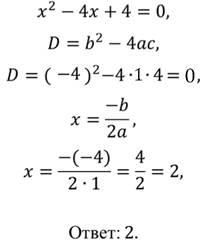
2.                Найдём корни второго квадратного трёхчлена:

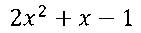
Решим квадратное уравнение:

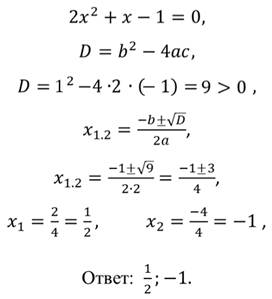
3.                Найдём корни ещё одного квадратного трёхчлена:

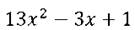
Решим квадратное уравнение:

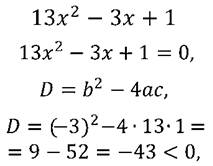
Ответ: корней нет.

Вывод:

Видим, что, как и квадратное уравнение, квадратный трёхчлен может иметь 1 корень, 2 корня или не иметь корней.

Решим задачу. Докажите, что из всех прямоугольников с периметром 20 сантиметров наибольшую площадь имеет квадрат.

Пусть х – одна сторона прямоугольника, 10 – х - вторая сторона прямоугольника. Тогда площадь прямоугольника равна х(10 – х).

Получаем:

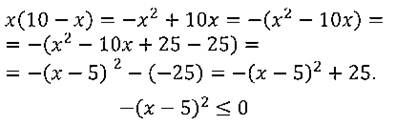
Последнее выражение принимает всегда неположительные значения, наибольшее из них:

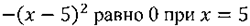
Соответственно наибольшая площадь будет у прямоугольника со стороной:

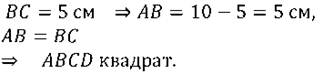
При решении задач с квадратным трёхчленом удобно использовать такое преобразование, как выделение квадрата.

Повторим их:

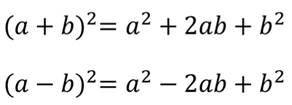
Потренируемся выделять квадрат двучлена из квадратного трёхчлена.

1.

2.