Тригонометрические тождества

Прежде, чем приступить к рассмотрению новой темы вспомним, что основным тригонометрическим тождеством называют равенство: .

Следующими формулами можно записать зависимость между синусом и косинусом, тангенсом и котангенсом, тангенсом и косинусом: , , , , , .

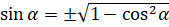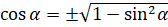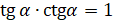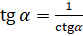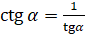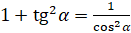Докажем с вами, что при 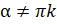, где 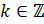, справедливо равенство: .

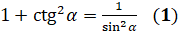Доказательство. Мы с вами знаем, что по определению 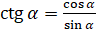. В левой части равенства  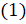запишем  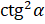как 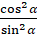:  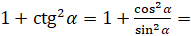[приведём слагаемые к общему знаменателю 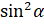]  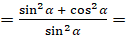[по основному тригонометрическому тождеству числитель равен 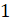] 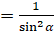. Таким образом, мы преобразовали левую часть равенства  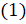к правой.

Так как делить на нуль нельзя, то 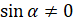, то есть 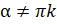, где .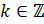

Равенство 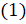 показывает нам зависимость между котангенсом и синусом.

Запомните! Равенство 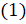, справедливое при всех допустимых значениях входящих в него букв (то есть таких, при которых его левая и правая части имеют смысл), называют тождеством, а задачи на доказательство таких равенств называют задачами на доказательство тождеств.

Доказанное тождество называют тригонометрическим тождеством.

Всегда ли при доказательстве тригонометрических тождеств нужно указывать допустимые значения углов? При доказательстве тригонометрических тождеств или при упрощении тригонометрических выражений чаще всего не указывают допустимые значения углов, если это не требуется в условии задачи.

Давайте докажем вот такое тождество: .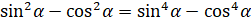

Доказательство. Запишем правую часть нашего тождества: 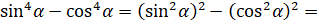 [применим формулу разности квадратов] 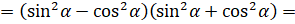[по основному тригонометрическому тождеству выражение во вторых скобках равно ] .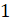

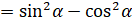Получается, что мы доказали данное тождество, преобразовав его правую часть к левой? Верно.

Докажем следующее тождество: .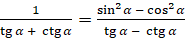

Чтобы доказать это тождество, мы докажем, что разность между его левой и правой частями равна нулю. Итак, запишем разность его левой и правой частей: 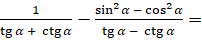 [так как 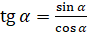, а 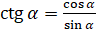, то запишем в наше выражение вместо  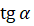и 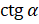 эти отношения]  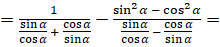[приведём дроби в знаменателе первого слагаемого к общему знаменателю. Затем приведём к общему знаменателю дроби в знаменателе второго слагаемого] 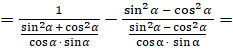 [в первом слагаемом разделим единицу на дробь в знаменателе. Во втором слагаемом разделим выражение в числителе на дробь в знаменателе] 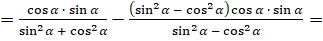 [по основному тригонометрическому тождеству знаменатель первого слагаемого равен 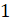. Во втором слагаемом сократим числитель и знаменатель на 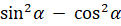] 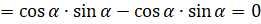. Таким образом, мы получили разность, которая равна нулю, то есть доказали наше тождество.

И докажем вот такое тождество: .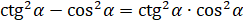

Доказательство. Преобразуем левую часть данного тождества. 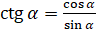. Тогда 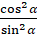:  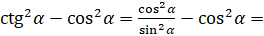[теперь приведём это выражение к общему знаменателю 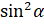]  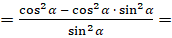[вынесем в числителе 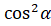]  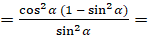[из основного тригонометрического тождества следует, что 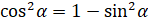. Тогда подставим в наше выражение  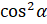вместо 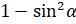]  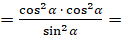[выполним умножение в числителе] .

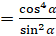Теперь преобразуем правую часть нашего тождества. Здесь также 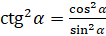:  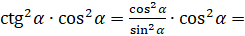[выполним умножение] .

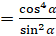Таким образом, мы получили, что левая и правая части нашего тождества равны одному и тому же выражению. А значит, тождество доказано? Да, данное тождество доказано.

Итак, вы, наверное, обратили внимание, что при доказательстве тождеств мы с вами применяли следующие способы: преобразование левой части тождества к правой. И, наоборот, преобразование правой части тождества к левой. Установление того, что разность между левой и правой частями тождества равна нулю. Преобразование левой и правой частей тождества к одному и тому же выражению.

А сейчас давайте выполним несколько заданий.

Задание первое. Докажите тождество: .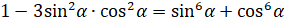

Доказательство.

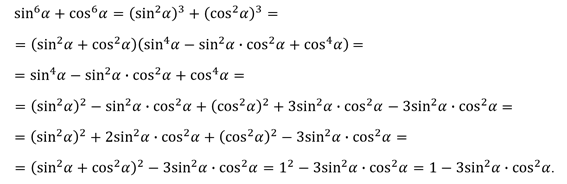
Задание второе. Упростите выражения: а) 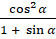; б) ;  .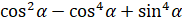

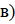
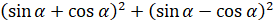Решение.