Вспомним,
что синусом угла 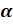 называется ордината точки
называется ордината точки 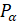 , полученной поворотом точки
, полученной поворотом точки 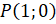 вокруг начала координат на угол
вокруг начала координат на угол 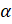 .
.
Косинусом угла 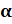 называется абсцисса точки
называется абсцисса точки 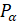 , полученной поворотом точки
, полученной поворотом точки 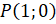 вокруг начала координат на угол
вокруг начала координат на угол 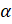 .
.
Тангенсом угла 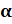 называется отношение синуса угла
называется отношение синуса угла 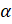 к его косинусу.
к его косинусу.
Котангенсом угла 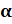 называется отношение косинуса угла
называется отношение косинуса угла 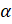 к его синусу.
к его синусу.
Также напомним, что оси координат делят плоскость на четыре четверти.
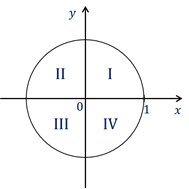
А сейчас давайте выясним, какие знаки имеют синус и косинус в зависимости от того, в какой четверти единичной окружности располагается точка.
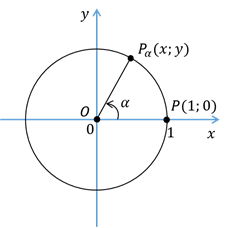
Пусть на координатной плоскости изображена единичная окружность с
центром в начале координат. Точка 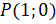 совершает поворот против часовой стрелки на угол
совершает поворот против часовой стрелки на угол 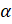 и оказывается в точке
и оказывается в точке 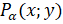 , которая расположена в первой четверти. Для точек, расположенных
в первой четверти, абсцисса и ордината положительны, а значит,
, которая расположена в первой четверти. Для точек, расположенных
в первой четверти, абсцисса и ордината положительны, а значит, 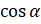 и
и 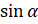 будут иметь положительные значения. То есть
будут иметь положительные значения. То есть 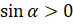 и
и 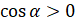 , если
, если 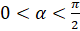 .
.
Пусть точка 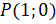 совершает поворот против часовой стрелки и оказывается в точке
совершает поворот против часовой стрелки и оказывается в точке 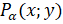 , которая расположена во второй четверти. Для точек, которые
расположены во второй четверти, абсциссы отрицательны, а ординаты положительны,
а значит,
, которая расположена во второй четверти. Для точек, которые
расположены во второй четверти, абсциссы отрицательны, а ординаты положительны,
а значит, 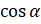 будет принимать отрицательные значения, а
будет принимать отрицательные значения, а 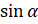 – положительные значения. То есть
– положительные значения. То есть 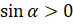 и
и 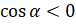 при
при 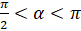 .
.
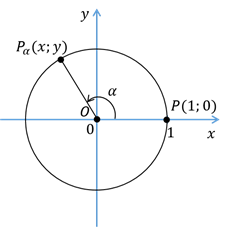
Теперь пусть точка 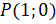 совершает поворот против часовой стрелки и оказывается в точке
совершает поворот против часовой стрелки и оказывается в точке 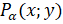 , которая расположена в третьей четверти. Для точек, которые
расположены в третьей четверти, абсциссы и ординаты отрицательны, а значит,
, которая расположена в третьей четверти. Для точек, которые
расположены в третьей четверти, абсциссы и ординаты отрицательны, а значит, 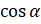 и
и 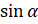 будут принимать отрицательные значения. То есть
будут принимать отрицательные значения. То есть 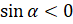 и
и 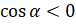 , если
, если 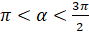 .
.
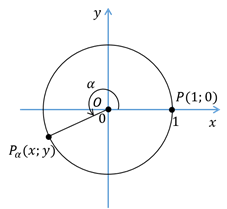
И пусть точка 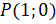 совершает поворот против часовой стрелки и оказывается в точке
совершает поворот против часовой стрелки и оказывается в точке 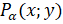 , которая расположена в четвёртой четверти. У точек, которые
расположены в четвёртой четверти, абсциссы положительны, а ординаты
отрицательны, а значит,
, которая расположена в четвёртой четверти. У точек, которые
расположены в четвёртой четверти, абсциссы положительны, а ординаты
отрицательны, а значит, 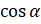 будет принимать положительные значения, а
будет принимать положительные значения, а 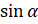 – отрицательные значения. То есть
– отрицательные значения. То есть 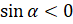 и
и 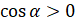 при
при 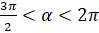 .
.

При этом важно помнить, что при повороте точки против часовой
стрелки на угол, больший 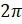 , а также при повороте точки по часовой стрелке на любой угол,
знаки синуса и косинуса определяются тем, в какой четверти окажется точка.
, а также при повороте точки по часовой стрелке на любой угол,
знаки синуса и косинуса определяются тем, в какой четверти окажется точка.
Давайте определим знаки синуса и косинуса углов: 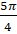 ,
, 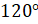 ,
, 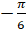 ,
, 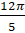 .
.
Итак, 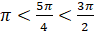 . Тогда углу
. Тогда углу 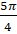 соответствует точка единичной окружности, расположенная в третьей
четверти. Мы с вами выяснили, что в третьей четверти синус и косинус принимают
отрицательные значения. Поэтому
соответствует точка единичной окружности, расположенная в третьей
четверти. Мы с вами выяснили, что в третьей четверти синус и косинус принимают
отрицательные значения. Поэтому 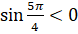 и
и 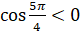 .
.
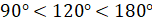 . А значит, углу в
. А значит, углу в 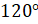 соответствует точка единичной окружности, расположенная во второй
четверти. Мы выяснили, что во второй четверти синус принимает положительные
значения, а косинус – отрицательные. Следовательно,
соответствует точка единичной окружности, расположенная во второй
четверти. Мы выяснили, что во второй четверти синус принимает положительные
значения, а косинус – отрицательные. Следовательно, 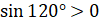 , а
, а 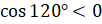 .
.
Углу 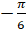 соответствует точка единичной окружности, расположенная в
четвёртой четверти. В четвёртой четверти синус принимает отрицательные
значения, а косинус – положительные. Следовательно,
соответствует точка единичной окружности, расположенная в
четвёртой четверти. В четвёртой четверти синус принимает отрицательные
значения, а косинус – положительные. Следовательно, 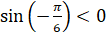 ,
, 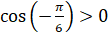 .
.
И последний угол – угол 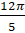 . Запишем
. Запишем 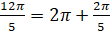 ,
, 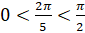 . Тогда можем сказать, что повороту точки с координатами
. Тогда можем сказать, что повороту точки с координатами 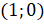 на угол д
на угол д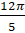 соответствует точка, расположенная в первой четверти. Поэтому
соответствует точка, расположенная в первой четверти. Поэтому 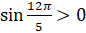 и
и 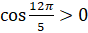 .
.
Давайте выясним, какие знаки имеет тангенс. Мы
знаем, что 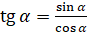 .
.
Если 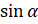 и
и 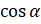 имеют одинаковые знаки, то
имеют одинаковые знаки, то 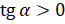 . Если же
. Если же 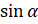 и
и 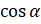 имеют разные знаки, то
имеют разные знаки, то  .
.
Итак, в первой четверти синус и косинус принимают положительные значения, то есть имеют одинаковые знаки, а значит, тангенс в первой четверти также принимает положительные значения.
Во второй четверти синус принимает положительные значения, а косинус – отрицательные, то есть они имеют разные знаки, а значит, тангенс принимает отрицательные значения во второй четверти.
В третьей четверти синус и косинус принимают отрицательные значения, то есть имеют одинаковые знаки. Следовательно, тангенс в третьей четверти принимает положительные значения.
В четвёртой четверти синус принимает отрицательные значения, а косинус – положительные, они имеют разные знаки. Следовательно, в четвёртой четверти тангенс принимает отрицательные значения.
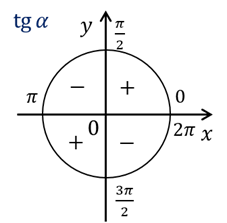
А какие знаки имеет котангенс? 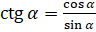 . А значит, если
. А значит, если 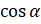 и
и 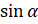 имеют одинаковые знаки, то
имеют одинаковые знаки, то 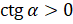 . Если
. Если 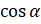 и
и 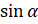 имеют разные знаки, то
имеют разные знаки, то 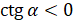 . Следовательно, значения котангенса имеют те же
знаки, что и значения тангенса.
. Следовательно, значения котангенса имеют те же
знаки, что и значения тангенса.
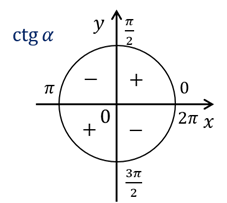
Давайте определим знаки тангенса и котангенса углов: 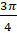 и
и 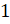 .
.
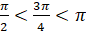 . Тогда углу
. Тогда углу 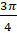 соответствует точка единичной окружности, расположенная во второй
четверти. Мы с вами выяснили, что во второй четверти тангенс и котангенс
принимают отрицательные значения. Поэтому
соответствует точка единичной окружности, расположенная во второй
четверти. Мы с вами выяснили, что во второй четверти тангенс и котангенс
принимают отрицательные значения. Поэтому 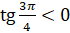 и
и 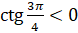 .
.
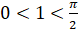 . А значит, углу, равному единице, соответствует точка единичной
окружности, расположенная в первой четверти. В первой четверти тангенс и
котангенс принимают положительные значения. Следовательно,
. А значит, углу, равному единице, соответствует точка единичной
окружности, расположенная в первой четверти. В первой четверти тангенс и
котангенс принимают положительные значения. Следовательно, 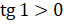 и
и 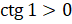 .
.
А сейчас давайте выполним несколько заданий.
Задание первое. Определите
знак числа 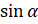 , если
, если 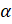 равняется:
равняется: 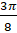 ,
, 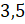 .
.
Решение.
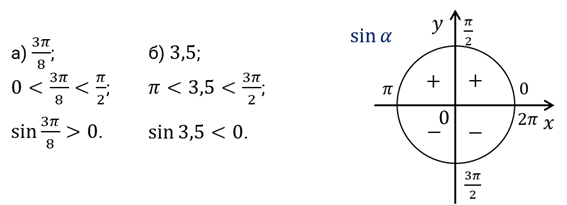
Второе задание. Определите
знак числа 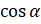 , если
, если 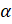 равняется:
равняется: 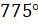 ,
, 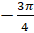 .
.
Решение.
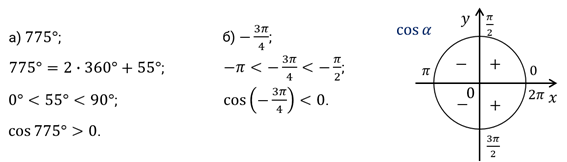
И ещё одно задание. Определите
знак числа 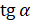 , если
, если 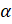 равняется:
равняется:  ,
, 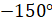 .
.
Решение.
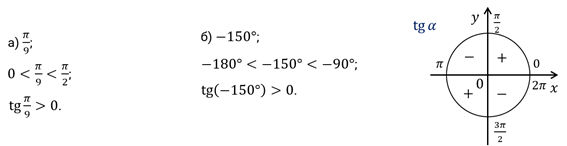

 Получите свидетельство
Получите свидетельство Вход
Вход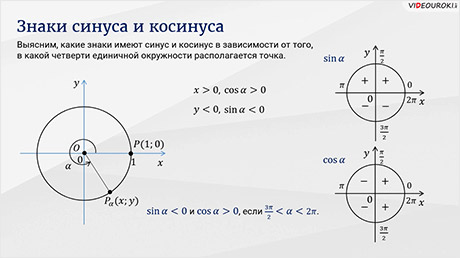



 0
0 14155
14155

