Закон сохранения импульса

Рассмотрим теперь простой пример: любая совокупность взаимодействующих тел может называться системой тел. Например, рюкзак и несущий его путник являются системой тел. На эти тела системы действуют внешние и внутренние силы.

Внутренние силы — это силы, возникающие в результате взаимодействия тел системы.

Внешние силы — это силы, возникающие в результате взаимодействия тел системы с телами, не принадлежащими этой системе.

Например, рюкзак давит на плечи путника своим весом — это пример внутренней силы. Также, на путника действует сила трения или сила сопротивления воздуха — это пример действия внешних сил. Запишем теперь импульсы тел системы, используя другую формулировку второго закона Ньютона:

Чтобы найти импульс системы нужно сложить импульсы каждого тела системы:

А теперь, обратите внимание, что равнодействующая сила, складывается из действия внешних и внутренних сил на каждое тело системы. Но, по третьему закону Ньютона, тела действуют друг на друга с силами, равными по модулю и противоположными по направлению. Иными словами, сумма внутренних сил системы всегда равна нулю:

Таким образом, мы выяснили, что изменить импульс системы тел могут только внешние силы. Отсюда вытекает формулировка закона сохранения импульса: если сумма внешних сил равна нулю, то импульс системы тел сохраняется (то есть остается неизменным):

где  — начальные скорости тел, а  — конечные скорости тел.

Эта формулировка закона сохранения импульса справедлива для системы, включающей в себя любое количество тел.

Все вы прекрасно знаете, что если столкнуть два мячика, направив их по одной прямой, то они обязательно, отскочат в разные стороны. Если мы предположим, что их массы равны, то можно с уверенностью утверждать, что скорости мячей будут равны по модулю и противоположны по направлению. Конечно, вы можете сказать, что мячи очень скоро остановятся, а, значит, потеряют свой импульс. Дело в том, что и на тот, и на другой мяч будет действовать сила трения, которая является внешней силой и способна изменить импульс системы. Если же мы предположим, что трение отсутствует, то мячи так и будут катиться с полученными скоростями, пока действие каких-либо других внешних сил не изменит их скорость.

Давайте рассмотрим частные случаи закона сохранения импульса для двух тел (поскольку в ближайшее время мы чаще всего будем рассматривать системы из двух тел). Существуют так называемые, абсолютно упругие и абсолютно неупругие удары.

При абсолютно неупругом ударе два тела сцепляются и продолжают движение как одно тело.

Абсолютно упругим ударом называется такой удар, при котором деформацией тел можно пренебречь (то есть сохраняется кинетическая энергия системы).

Ярким примером демонстрации закона сохранения импульса является механическая система, получившая название «колыбель Ньютона».

В этой системе силы трения практически отсутствуют, поэтому, требуется достаточно длительное время, чтобы шарики остановились. Удары этих шаров вполне можно считать абсолютно упругими.

Примеры решения задач.

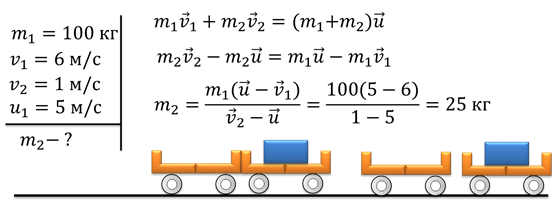
Задача 1. Из пушки массой 600 кг произвели выстрел, после чего, пушка откатилась назад со скоростью 4 м/с. Учитывая, что ствол пушки расположен горизонтально, какова скорость снаряда, массой 50 кг?

Задача 2. Груженая тележка массой 100 кг, едет со скоростью 6 м/с. Впереди неё в том же направлении катится вторая тележка со скоростью 1 м/с. После абсолютно неупругого удара скорость груженой тележки равна 5 м/с. Найдите массу второй тележки.

В первую очередь, обратите внимание, что мы рассматриваем абсолютно неупругий удар. То есть, после столкновения две тележки продолжили катиться как одно тело. А это значит, что скорость первой тележки, конечно же, равна скорости второй тележки.