Мы с вами уже знаем
несколько формул для вычисления площади треугольника. Давайте вспомним их. Если
мы знаем длину одной из сторон треугольника и длину высоты, проведенной к этой
стороне, то площадь треугольника можно найти как половина произведения этих
длин  .
.

Например, найдем
площадь треугольника, показанного на рисунке при h= 6,
а a=5. Площадь этого треугольника  .
.
Если треугольник
прямоугольный, то его площадь находится как половина произведения катетов 
Например, найдем
площадь прямоугольного треугольника с катетами равными 4 и 9. Площадь  .
.
Если нам известны длины всех сторон треугольника, то площадь можно вычислить по формуле Герона, где p – полупериметр треугольника.

 .
.
Найдем, например,
площадь треугольника со сторонами 13, 14 и 15 сантиметров. Полупериметр этого
треугольника  .
Тогда площадь этого треугольника по формуле Герона
.
Тогда площадь этого треугольника по формуле Герона
 .
.
Сегодня на уроке мы с вами познакомимся еще с одной формулой, но сначала давайте вспомним формулу для координат произвольной точки А, расположенной в верхней полуплоскости.

Рассмотрим произвольный треугольник ABC со сторонами a, b, c и углами α, β, γ.
Докажем, что
площадь треугольника вычисляется по формуле  .
.
Расположим треугольник ABC в координатной плоскости так, чтобы точка C совпадала с началом координат, а точка B лежала на положительной полуоси Cx, а точка А имела положительную ординату, то есть располагалась в верхней полуплоскости.

Опустим из точки А высоту h. Площадь этого треугольника равна половине произведения
стороны a на h. Координаты
точки А равны
 .
.
Высота h
будет равна ординате точки А, то есть равна произведению длины стороны АC на синус угла γ, или  .
.
Таким образом, мы доказали теорему. Сформулируем ее.
Теорема. Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.

Нетрудно убедиться,
что если с началом координат совместить точку А, точку C расположить на положительном полуоси Ax,
а точку B расположить в верхней
полуплоскости, то можно записать, что площадь треугольника  .
.

Если же с началом
координат совместить точку B, точку А расположить на
положительной полуоси Bx, а точку C расположить в верхней полуплоскости, тогда площадь
треугольника  .
.

Нетрудно заметить, что формула для
вычисления площади прямоугольного треугольника является частным случаем этой
формулы. Рассмотрим прямоугольный треугольник. Применяя общую формулу для
вычисления площади треугольника, получим, что площадь этого  . Угол
C – прямой, его синус равен 1, то есть площадь
прямоугольного треугольника равна половине произведения катетов
. Угол
C – прямой, его синус равен 1, то есть площадь
прямоугольного треугольника равна половине произведения катетов  . Мы
получили, уже известную нам формулу.
. Мы
получили, уже известную нам формулу.
Решим несколько задач.
Задача. Найти
площадь треугольника  если:
если:
а)  ,
, 
 ; б)
; б)  ,
, 
 ;
;
в)  ,
, 
 .
.
Решение.

Запишем формулу для вычисления площади треугольника.

а) 


б) 


в) 


Поскольку 46 – не табличное значение, то можно оставить в таком виде. Или с помощью калькулятора найти приближенное значение синуса 46°. Тогда получим, площадь треугольника приблизительно равна 40,28 сантиметрам квадратным.
Задача.  .
Найти
.
Найти  , если
, если
 ,
,  .
.
Решение.






Теперь давайте рассмотрим параллелограмм ABCD.

Проведем диагональ АC. Эта диагональ делит параллелограмм на два треугольника.
Легко увидеть, что эти треугольники равны по третьему признаку (стороны AB и CD, АD и
BC равны по свойству сторон параллелограмма, АC – общая). Площадь треугольника ABC
можно найти по формуле:  .
Площадь треугольника ACD можно найти по формуле:
.
Площадь треугольника ACD можно найти по формуле:  .
Тогда площадь параллелограмма равна сумме площадей этих треугольников
.
Тогда площадь параллелограмма равна сумме площадей этих треугольников  .
.
 ,
,  .
.
То есть, другими словами, площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними.
И опять, как в случае с треугольником, формула для вычисления площади прямоугольника является частным случаем формулы для вычисления площади параллелограмма. Прямоугольник – параллелограмм, углы которого равны 90°.



Обратите внимание, что угол между сторонами параллелограмма можно записать так.
Задача. Найти
площадь параллелограмма  если:
если:
 ,
, 
 .
.
Решение.



Задача. Соседние
стороны параллелограмма равны  ,
,  .
Какой угол должен быть между ними, чтобы площадь параллелограмма была
наибольшей?
.
Какой угол должен быть между ними, чтобы площадь параллелограмма была
наибольшей?
Решение.




Таким образом мы получили, что наибольшей будет площадь прямоугольника со сторонами a и b.
Задача. Найти
площадь ромба, если его стороны равны  , а
один из углов равен
, а
один из углов равен  .
.
Решение.
Ромб – параллелограмм, значит, для вычисления площади ромба мы можем использовать формулу для вычисления площади параллелограмма.




Задача. Площадь
треугольника  равна
равна
 .
Сторона
.
Сторона  в 2
раза больше стороны
в 2
раза больше стороны 
 .
Найти
.
Найти  .
.
Решение.




Подведем итоги урока:
Сегодня на уроке, мы вспомнили формулы для вычисления площади треугольника, а также познакомились с новой. Мы познакомились с формулой вычисления площади параллелограмма. Рассмотрели примеры применения этих формул.

 Получите свидетельство
Получите свидетельство Вход
Вход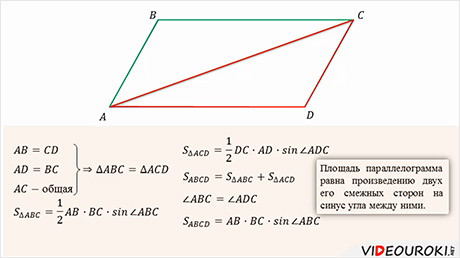



 0
0 11168
11168


