Прежде чем приступить к изучению нового материала, давайте вспомним, что
Для любого угла  синусом
угла
синусом
угла  называется
ордината
называется
ордината  точки
М,
точки
М,
а косинусом угла
 –
абсцисса
–
абсцисса  точки
М.
точки
М.
Тангенсом угла  называется
называется
 .
.
Котангенсом угла
 называется
называется
 .
.
 основное
тригонометрическое тождество
основное
тригонометрическое тождество
Если  ,
то:
,
то: 
Если  ,
то:
,
то: 
Еще сегодня нам надо вспомнить о том, что координаты векторы равны разности соответствующих координат его конца и начала.
Координаты вектора  равны
разности соответствующих координат его конца
равны
разности соответствующих координат его конца и
начала
и
начала  :
:
 .
.
Еще вспомним лемму о коллинеарных векторах.
Лемма. Если
векторы  и
и
 коллинеарны
и
коллинеарны
и  ,
то существует такое число
,
то существует такое число  ,
что
,
что  .
.
Рассмотрим задачу. Определить координаты точки А, которая расположена в верхней координатной полуплоскости.

Построим в этой полуплоскости
единичную полуокружность. Соединим точку А с центром полуокружности и обозначим
за М точку пересечения отрезка ОА с полуокружности. Координаты точки М ( .
.
Определим
координаты вектора  ,
поскольку координаты точки О (0;0).
,
поскольку координаты точки О (0;0).
 ,
,


С другой стороны,


Теперь давайте проанализируем знаки координат точки А.
Координаты точки зависят от
величины отрезка ОА, (а это всегда положительное число), и от знака синуса и
косинуса угла α. Синус произвольного угла из промежутка от 0 до 180
градусов находится в промежутке от 0 до 1, то есть принимает не отрицательные
значения. Косинус угла может принимать значения от -1 до 1, то есть быть как
положительным, так и отрицательным. Значит, можно записать, что  ;
;
 ;
;
 .
.
Решим несколько задач.
Задача. Угол
между лучом  ,
пересекающим единичную полуокружность, и положительной полуосью
,
пересекающим единичную полуокружность, и положительной полуосью  равен
равен
 .
Найдите координаты точки
.
Найдите координаты точки  ,
если:
,
если:
а)  ,
,
 ;
б)
;
б)  ,
,
 ;
в)
;
в)  ,
,
 .
.
Решение.


а) 



б) 



в) 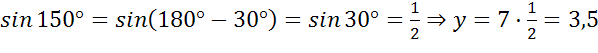


Задача. Найти
угол между лучом  и
положительной полуосью
и
положительной полуосью  ,
если:
,
если:
а)  ;
б)
;
б)  ;
в)
;
в)  ;
г)
;
г)  .
.
Решение.




Запишем формулы для определения координат точки А.



а) 



б) 



в) 



г) 



Подведем итоги урока. Сегодня на уроке мы вывели формулы для вычисления координат точки и рассмотрели, как они используются при решении задач.

 Получите свидетельство
Получите свидетельство Вход
Вход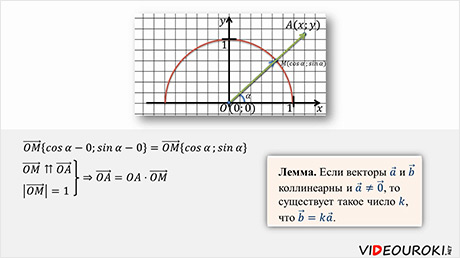



 0
0 20209
20209


