Прежде чем приступить к изучению нового материала, давайте вспомним формулы для нахождения площади треугольника и параллелограмма.
Формулы для вычисления площади треугольника:




Формулы для вычисления площади параллелограмма:


Сегодня на уроке мы с вами рассмотрим теорему синусов.
Теорема. Стороны треугольника пропорциональны синусам противолежащих углов.
Доказательство.
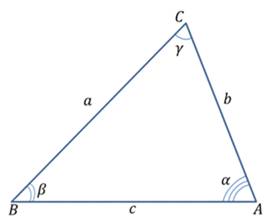
1.  ,
,  ,
, 


2. 


Таким образом, мы получили что отношения длины стороны на синус противолежащего угла равны.
Доказать, что отношение стороны треугольника к синусу противолежащего угла равно диаметру описанной окружности.

Доказательство.

1.  и
и  − совпадают
− совпадают
 прямоугольный
прямоугольный

2.  и
и  − лежат с одной
стороны от
− лежат с одной
стороны от 
 прямоугольный
прямоугольный


3.  и
и  − лежат по разные
стороны от
− лежат по разные
стороны от 


Что и требовалось доказать.
Из доказательства этих двух
утверждений следует, что  . Это утверждение
называется расширенной теоремой синусов.
. Это утверждение
называется расширенной теоремой синусов.

Решим несколько задач.
Задача. Найти
 треугольника
треугольника  , если
, если  ,
,  ,
,  .
.
Решение.




 или
или 
Ответ:  или
или  .
.
Задача. Найти
длину стороны  треугольника
треугольника  , если
, если  ,
,  ,
,  .
.
Решение.



Ответ:  .
.
Задача. В
треугольнике  углы
углы  . Найти длину
. Найти длину  , если
, если  .
.
Решение.

 ,
, 







Ответ:  см.
см.
Задача. Сторона
 треугольника
треугольника  равна
равна  сантиметрам, а
сантиметрам, а  . Найти радиус окружности,
описанной около треугольника.
. Найти радиус окружности,
описанной около треугольника.
Решение.





Ответ:  см.
см.
Задача. В
окружность с  вписан четырехугольник.
Два из его углов равны
вписан четырехугольник.
Два из его углов равны  и
и  . Найти диагонали этого
четырехугольника.
. Найти диагонали этого
четырехугольника.
Решение.







Ответ:  см,
см,  см.
см.
Подведем итоги урока. Сегодня на уроке мы доказали теорему синусов, расширенную теорему синусов и рассмотрели применение этих теорем на конкретных примерах.

 Получите свидетельство
Получите свидетельство Вход
Вход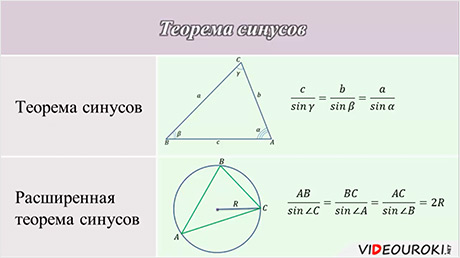



 0
0 8474
8474