Прежде чем приступить к изучению нового материала, давайте, вспомним: формулы для вычисления площади треугольника и параллелограмма.
Формулы для вычисления площади треугольника:




Формулы для вычисления площади параллелограмма:


Теорема синусов:
Стороны треугольника пропорциональны синусам противолежащих углов.

Расширенная теорема синусов:

Расстояние между двумя точками:

Сегодня на уроке мы с вами сформулируем и докажем теорему косинусов.
Теорема. Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон, умноженное на косинус
угла между ними.

Докажем это.







Что и требовалось доказать.
Частным случаем теоремы косинусов является теорема Пифагора.
Давайте рассмотрим прямоугольный треугольник и запишем для него теорему косинусов.

 ,
, 

Именно поэтому теорему косинусов называют обобщенной теоремой Пифагора.
Задача. Найти
сторону  треугольника
треугольника  , если:
, если:
а)  ,
, 
 ; б)
; б)  ,
, 
 ;
;
в)  ,
, 
 .
.
Решение.
Запишем теорему косинуса для стороны AB.


а) 


б) 



в) 


Задача. Найти
косинус наибольшего угла треугольника  , если стороны этого
треугольника равны: а)
, если стороны этого
треугольника равны: а)  ,
,  ,
,  ; б)
; б)  ,
,  ,
,  ;
;
в)  ,
,  ,
,  .
.
Решение.


а) 

 −
треугольник остроугольный
−
треугольник остроугольный
б) 

 −
треугольник тупоугольный
−
треугольник тупоугольный
в) 

 − треугольник
прямоугольный
− треугольник
прямоугольный
Давайте подробнее рассмотрим выражения для косинуса угла.

В знаменателе дроби всегда находится положительное число, потому что стороны треугольника могут иметь только положительные длины. Значит, знак косинуса зависит от числителя. В числителе у нас находится разность.
Пусть  наибольшая сторона
треугольника, тогда если:
наибольшая сторона
треугольника, тогда если:
ü
 , то треугольник
остроугольный
, то треугольник
остроугольный
ü
 , то треугольник
прямоугольный
, то треугольник
прямоугольный
ü
 , то треугольник
тупоугольный
, то треугольник
тупоугольный
Задача. Определить вид треугольника со сторонами:
а) 23, 25, 34; б) 7, 24, 25; в) 6, 7, 9.
Решение.
Эту задачу мы будем решать двумя способами: с помощью только что сформулированных утверждений и вычислив косинус наибольшего угла.
а) Решая первым
способом, мы получим, что в первом случае у нас тупоугольный треугольник.  ,
, 
 треугольник
тупоугольный.
треугольник
тупоугольный.
Давайте проверим это.

Косинус отрицательный, значит, наибольший угол треугольника – тупой, то есть треугольник тупоугольный.
б)  ,
, 
 треугольник
прямоугольный
треугольник
прямоугольный

в)  ,
, 
 треугольник
остроугольный
треугольник
остроугольный

Решая эту задачу, мы убедились в том, что утверждения действительно справедливы для любого треугольника. Эти утверждения называют следствием из теоремы косинусов.
Пусть  наибольшая сторона
треугольника, тогда если:
наибольшая сторона
треугольника, тогда если:
ü
 , то треугольник
остроугольный
, то треугольник
остроугольный
ü
 , то треугольник
прямоугольный
, то треугольник
прямоугольный
ü
 , то треугольник
тупоугольный
, то треугольник
тупоугольный
Задача. Доказать, что для произвольного треугольника справедлива формула:
 .
.
Доказательство.








Это формула называется формулой медиан треугольника.
Задача. В
треугольнике  найти длины всех
медиан, если
найти длины всех
медиан, если  ,
,  ,
,  .
.
Решение. Воспользуемся только что доказанной формулой. Очевидно, что будут выполняться аналогичные формулы для медиан к сторонам b и c. Тогда несложно вычислить длины всех медиан треугольника…






Задача. Доказать,
что для любого параллелограмма  .
.
Решение.








Задача. Стороны
параллелограмма равны  и
и  . Одна из диагоналей
равна
. Одна из диагоналей
равна  . Найти вторую
диагональ.
. Найти вторую
диагональ.
Решение.
Воспользуемся только что доказанным утверждением.





Задача. Две
стороны треугольника равны  и
и  ,
,  . Найти третью сторону
треугольника.
. Найти третью сторону
треугольника.
Решение.

Для нахождения неизвестной стороны, воспользуемся теоремой косинуса.

Запишем основное тригонометрическое тождество и найдем, что


 или
или 



Подведем итоги урока. Сегодня на уроке мы сформулировали и доказали теорему косинусов. Вывели следствие их этой теоремы. Познакомились с формулой для нахождения длины медианы треугольников, а также познакомились с формулой связывающей диагонали и стороны параллелограмма.

 Получите свидетельство
Получите свидетельство Вход
Вход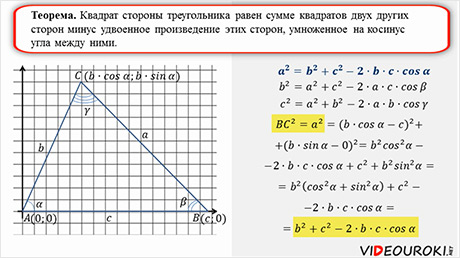



 0
0 8542
8542