Сегодня на уроке мы подытожим наши знания по разделу «Соотношения между сторонами и углами треугольника».
Прежде чем приступить к решению задач, давайте вспомним основной теоритический материал этой темы.
Формула для вычисления площади треугольника:

Теорема косинусов:

Теорема синусов: Стороны треугольника пропорциональны синусам противолежащих углов.

Расширенная теорема синусов:

Решить треугольник – это значит найти все его элементы (три стороны и три угла) по каким-нибудь известным трем элементам, определяющим треугольник.
К задачам такого плана относятся следующие задачи: решение треугольника по трем сторонам; решение треугольника по трем углам; решение треугольника по двум сторонам и углу между ними; решение треугольника по двум сторонам и углу, не лежащего между ними; решение треугольника по стороне и прилежащим к ней углам; решение треугольников по стороне и произвольным двум углам.
Рассмотрим каждый вид таких задач отдельно.
Начнем с решения треугольника по трем углам.

Запишем теорему синусов и косинусов и подумаем, с помощью какой из них можно решить треугольник.


Обе эти теоремы содержат длины сторон, поэтому зная только углы треугольника нельзя найти длины сторон треугольника.
Попробуем теперь решить треугольник по трем сторонам.
Зная длины всех сторон треугольника, по теореме косинусов можно найти косинусы всех углов треугольника. А, зная косинус угла, сам угол найти несложно. Для этого можно воспользоваться либо калькулятором либо таблицами Брадиса.






Значит в этом случае решить треугольник можно с помощью теоремы косинусов.
Рассмотрим пример.
Задача. Найти углы треугольника, если стороны треугольника равны 25, 20, 17.
Решение.







Ответ:  ;
;  ;
;  .
.
Следующим мы рассмотрим решение треугольника по стороне и прилежащим к ней углам.
Сразу замечаем, что
третий угол найти нетрудно, он равен разности 180° и известных углов  .
.
Запишем теорему синусов.



Из каждого равенства, мы можем найти сторону треугольника. Таким образом, зная длину одной стороны и величину двух прилежащих к ней углов, можно найти все остальные элементы треугольника, используя теорему синусов.









Задача. Решить
треугольник, если одна из сторон треугольника равна  , а углы
прилежащие к этой стороне равны
, а углы
прилежащие к этой стороне равны  и
и
 °
соответственно.
°
соответственно.
Решение.






Ответ: 

 .
.
Задача. Решить
треугольник если две стороны его равны  см и
см и  см
соответственно, а угол между ними равен
см
соответственно, а угол между ними равен  .
.
Решение.






Ответ: 

 .
.
Теперь давайте посмотрим, а можно ли решить треугольник, если мы знаем две стороны и угол, который не лежит между ними. Да, можно. Для этого по теореме синусов надо найти второй угол треугольника, а затем и третий угол и по теореме косинусов найти третью сторону треугольника.




То есть и в этом случае треугольник можно решить с помощью теоремы синусов или теоремы косинусов.
Задача. Решить
треугольник, если две его стороны равны  и
и  , а один из
углов, не лежащий между этими сторонами, равен
, а один из
углов, не лежащий между этими сторонами, равен  .
.
Решение.







Ответ: 
 .
.
Итак, давайте обобщим.
Если в треугольнике известны величины трех углов, то решить его нельзя.
Если в треугольнике известны три стороны, то решить такой треугольник можно по теореме косинусов.
Если в треугольнике известна сторона и два любых угла, то решить такой треугольник можно с помощью теоремы синусов.
Если в треугольнике известны две стороны и угол между ними, то решить такой треугольник можно с помощью теоремы косинусов или теоремы синусов.
Если же нам известны две стороны и любой угол, который не лежит между ними, то треугольник можно решить по теореме синусов и косинусов.

 Получите свидетельство
Получите свидетельство Вход
Вход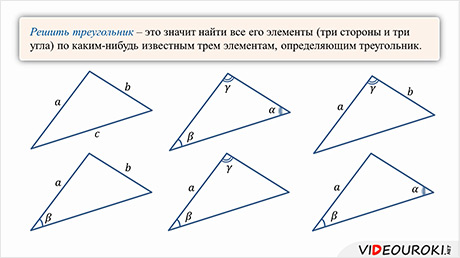



 1
1 25959
25959


Супер)