Тема нашего урока «Граф. Вершины и ребра графа». И эта тема у нас сегодня неспроста.

Посмотрите, это Пчёла и Скрути – верные друзья принцессы Амели. И вот какая приключилась с ними история.
Их любимую принцессу захватил и держит взаперти злодей Граф Дерби в своём графстве. И освободит её только при одном условии.

Ему нужна одна необычная статуя, говорят она волшебная.

Но как найти эту статую, если все её части находятся в разных местах планеты?
Ага, Граф Дерби дал карту, на которой указаны все места нахождения частей статуи и сову, которая будет подсказывать дорогу. Пчёлу и Скрути надо доставить статую до утра, пока граф спит.

– Надеюсь, успеем, – говорит Пчёл. У меня есть крылья, а Скрути летает на метле, так что с перемещением по планете проблем не будет, самолёт заказывать не придётся…
– Ну, что ж, давай внимательно рассмотрим карту, найдём место, где мы находимся, – говорит Скрути. И вперёд, спасать принцессу!
– Ну, сова, говори, куда лететь.
– Летите туда, где дом стоит на берегу озера среди глухого леса. Лишь один лебедь в нём живёт. И там найдёте первую часть статуи.
– Полетели! А вот и первая часть. Куда дальше лететь, сова?
– Вторая часть лежит там, где среди статуй необычных стоит дом высотный.
– Ура! У нас есть и вторая часть!
– А теперь надо туда, где нет воды, и стоят геометрические фигуры их песка.
– Взяли третью часть. Нам надо торопиться, время близится к утру. Куда дальше?
– Среди гор длинная дорога ведёт к четвёртой части статуи.
– Осталась одна часть статуи и принцесса будет спасена.
– Чтобы взять последнюю часть статуи, надо перейти через мостик.
– Ура, все части статуи у нас, – говорит Пчёл. Давай соберём их и посмотрим, что это за статуя такая.

– Да-а-а, какая интересная статуя, – говорит Скрути. Действительно она, наверное, волшебная. Будем надеяться, что Граф Дерби своё обещание выполнит и вернёт нам принцессу. Возвращаемся назад в графство, оставляем статую и ждём!
Ура! Мы спасли принцессу!

Она теперь вместе со своими верными друзьями Пчёлой и Скрути. Они будут играть и веселиться, а мы давайте разберёмся, как же это связано с нашей темой.
Подумайте, на что похожа наша карта?

На карту дорог, на план, на схему.
А если мы нашу карту немного преобразим…

Такие схемы в математике и информатике называются графом.
Как вы думаете, чем граф отличается от карты? На нём нет ничего, кроме точек и линий.
Точки называются вершинами графа.
А линии, которые связывают вершины, называются рёбрами графа.
Значит, граф – это множество точек, которые могут соединяться линиями. Линия указывает на связь между двумя точками.

А давайте рассмотрим ещё одну карту и описание к ней.
Кто ходит в гости по утрам,
Тот поступает мудро.
Известно всем, тарам-парам,
На то оно и утро!
Мы знаем, Винни-Пух очень любит ходить в гости.

Вот и на этот раз, Вини-Пух вышел рано утром из дома, зашёл в гости к Сове, потом к Кролику. Затем зашёл в лес собрал грибов, около озера поговорил с Осликом Иа, а потом зашёл в гости к Пятачку.

Давайте построим граф, который будет отображать утренний маршрут Винни-Пуха.
Давайте подумаем, какие объекты будут вершинами графа? Дом Винни-Пуха, Сова, Кролик, лес, Ослик Иа, Пятачок.

Обратите внимание, что вершины обозначены заглавными буквами, и каждая вершина имеет своё обозначение.
А теперь надо соединить вершины так, чтобы рёбра графа отображали путь, по которому шёл Винни-Пух. Итак. Винни-Пух вышел из дома и зашёл в Сове, значит соединяем эти две вершины. После Совы Винни-Пух зашёл к Кролику, соединяем вершины Сову и Кролика. Затем зашёл в лес, к Ослику Иа и к Пятачку. Граф построен и весь путь Винни-Пуха отображён.
Винни –Пух любит ходит в гости. А представьте, что вы всем классом собрались… нет не в гости, а в путешествие в город Н. У вас есть граф, на котором вершины графа обозначают места, которые вы должны обязательно посетить и есть описание этого города. Вам необходимо по описанию города соединить вершины графа, чтобы затем без труда найти нужное место.
Вы уже знаете, что вершины графа можно обозначать заглавными буквами. А вот и подсказка, что означают эти заглавные буквы: парк, фонтаны, цирк, музей, аквапарк, торговый центр, зоопарк, вокзал.
Итак, читаем описание и соединяем вершины графа.

От парка одна улица ведёт к цирку, другая к фонтанам, а третья – к музею. Есть улица, ведущая от музея к аквапарку, а от фонтанов можно дойти к зоопарку. Улица между аквапарком и зоопарком называется Графской, а между аквапарком и вокзалом есть Вокзальная улица. По Рёберной улице можно дойти от вокзала к торговому центру, а по Вершинной улице – от торгового центра к музею.
Граф построен, вершины соединили. И вы смело можете ехать в путешествие в город Н.

Вот друзья Юля, Игорь, Андрей, Маша собираются в путешествие и берут с собой фрукты.

Юля любит бананы, киви, виноград. Игорь ест только яблоки и груши. А Андрей ест бананы, яблоки, груши и виноград. Маша обожает киви и бананы. Давайте изобразим графом вкусы ребят. В нашем графе вершинами будут ребята и все фрукты, которые они любят.
Итак!
Юля любит бананы, киви, виноград. Значит проводим ребра от вершины Ю к вершинам, Б, К и В.
Игорь ест только яблоки и груши. Связываем вершину И с вершинами Я и Г.
Андрей ест бананы, яблоки, груши и виноград.
Маша обожает киви и бананы.
Наш граф построен!

И ребята могут ехать в путешествие, а мы сделаем выводы из нашего урока.
Ребята, сегодня на уроке вы узнали следующие новые слова.
Граф, вершина графа, ребра графа.
Граф – это множество точек, которые могут соединяться линиями.
Точки называются вершинами графа.
А линии, которые связывают вершины, называются рёбрами графа.
Что могут обозначать вершины графа? Объекты, которые связаны между собой. В наших примерах это были достопримечательности в городе, имена и фрукты.
Что обозначают ребра графа? Связь между объектами.
Выводы сделаны, и я надеюсь, что трудностей при построении графов у вас не возникнет. Успехов вам!

 Получите свидетельство
Получите свидетельство Вход
Вход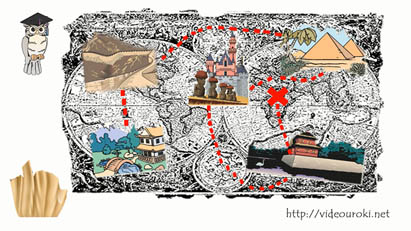



 0
0 4574
4574


