Истинность высказываний со словами «И», «ИЛИ»

Это бабочка?

Как она вообще здесь появилась?

Оказывается, один очень умный профессор по фамилии Бабочкин разводил в своей домашней лаборатории бабочек разных видов.

А однажды, он сотворил немыслимое чудо – волшебную бабочку, которая умеет писать. Она прилетела к нам сегодня на урок и поможет изучать тему «Истинность высказывания со словами «и», «или»».

Бабочка, а давай поиграем в игру «Верно – неверно». Мы тебе будем читать некоторые высказывания, а ты, если согласна с этим высказыванием, садись на кнопку с надписью «ВЕРНО», а если не согласна – с надписью «НЕВЕРНО». Бабочка согласилась!

Итак, первое высказывание!

Сегодня 32 октября. Интересно, куда сядет бабочка? Конечно, неверно, 32 октября не бывает.

Яблоки и груши – фрукты. Конечно, верно.
Самый короткий месяц в году длится 28 дней. Конечно, верно. Действительно, в феврале 28 дней, лишь один раз в 4 года в феврале 29 дней. Вот не повезло тому, у кого день рождение 29 февраля…

Белка и Стрелка – это имена собак, которые летали в космос. Правильно, верно.

Все птицы умеют летать. Конечно, неверно. Например, пингвины, страусы летать не умеют, а ведь это птицы.

Посмотрите ещё раз на высказывания и на ответы бабочки…

На одни высказывания бабочка отвечала «верно», потому что они соответствует действительности, это правда. А на другие высказывания бабочка отвечала «неверно», т.к. они действительности не соответствуют, это неправда.

А как ещё можно назвать эти высказывания?

Мы уже знаем, если высказывание соответствует действительности, т.е. в высказывании содержится правдивая информация, то это истинное высказывание. А если высказывание действительности не соответствует, т.е. в высказывании содержится неверная информация, то такое высказывание является ложным.

Значит, те высказывания, которые бабочка обозначила словом «верно» можно назвать истинными. А обозначенные словом «не верно» ̶ ложными.

А может быть теперь бабочка напишет высказывание, а мы попробуем определить истинное оно или ложное?

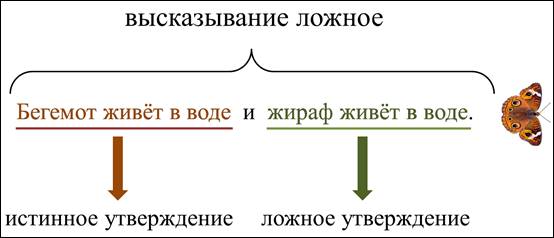
Бегемот живёт в воде и жираф живёт в воде.

Из скольких утверждений построено данное высказывание? Из двух. Первое «бегемот живёт в воде», а второе ̶ «жираф живёт в воде». И эти два утверждения соединены словом «и».

Ребята, высказывания, которые состоят из нескольких утверждений, называются составными. В них утверждается не одно, а несколько утверждений. И чтобы определить истинность такого высказывания, надо определить истинность каждого утверждения, из которых состоит это высказывание.

Определим его истинность первого утверждения в нашем высказывании: бегемот живёт в воде. Это утверждение истинно, т.к. бегемот действительно живёт в воде.

А теперь определим истинность второго утверждения: жираф живёт в воде. Это утверждение ложно, т.к. жираф в воде не живёт, он живёт на суше.

Так что получается, одно утверждение в высказывании истинно, а другое ложно. Так а высказывание тогда какое: истинное или ложное?

Если в составном высказывании со словом «и» одно из утверждений ложное, тогда ложное и всё высказывание. В нашем высказывании одно утверждение истинное, а другое ложное, значит, всё высказывание ложное.

Теперь второе высказывание.

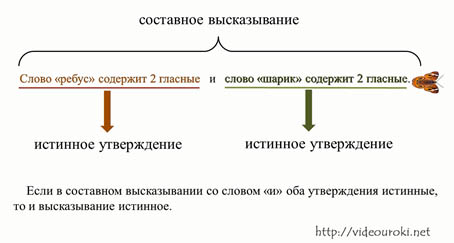
Слово «ребус» содержит 2 гласные и слово «шарик» содержит 2 гласные.

Это опять составное высказывание, т.к. состоит из двух утверждений, которые соединяются словом «и».

Давайте определим истинность этого высказывания. Для начала определим истинность каждого из утверждений, входящих в высказывание. Начнём с первого: слово «ребус» содержит 2 гласные. Это истинное утверждение.

Слово «шарик» содержит 2 гласные – и это истинное утверждение.

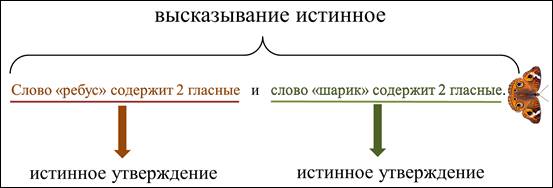
Если в составном высказывании со словом «и» оба утверждения истинные, то и высказывание истинное.

Ещё одно высказывание.

Пионы бывают белого цвета или пионы бывают синего цвета.

Это тоже составное высказывание. А чем оно отличается от двух предыдущих высказываний? В предыдущих высказываниях утверждения соединялись словом «и». А в этом высказывании соединяются словом «или».

Но, как и в предыдущих высказываниях, чтобы оценить истинность высказывания, необходимо оценить истинность каждого утверждения отдельно.

Пионы бывают белого цвета. Это истинное утверждение. Пионы бывают синего цвета. Это ложное утверждение.

Если в составном высказывании со словом «или» одно из утверждений истинное, то такое высказывание тоже истинное. В высказывании «Пионы бывают белого цвета или пионы бываю синего цвета» одно утверждение истинное, значит и всё высказывание истинное.

И последнее высказывание.

На южном полюсе всегда идёт снег или на южном полюсе всегда жарко.

И это составное высказывание, т.к. два утверждения соединены словом «или».

И чтобы определить его истинность, определяем истинность двух его утверждений отдельно.

На южном полюсе всегда идёт снег – это ложное высказывание, так как снег идёт не каждый день. На южном полюсе всегда жарко – и это ложное высказывание. Потому что там всегда холодно.

Если в составном высказывании со словом «или» оба утверждения ложные, то всё высказывание тоже ложное. Значит, наше высказывание ложное.

Давайте повторим то, что мы узнали.

Составное высказывание состоит из нескольких утверждений, которые соединяются словом «и» или словом «или».

А давайте с вами договоримся истинные высказывания отмечать большой буквой И, а ложные – большой буквой Л.

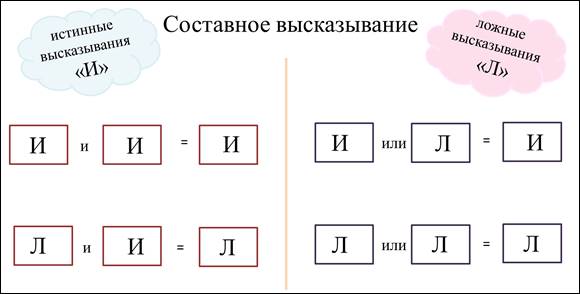
Итак! Высказывание со словом «и» истинное тогда, когда истинные оба утверждения.

Высказывание со словом «или» истинное тогда, когда истинное хотя бы одно из утверждений.

Высказывание со словом «и» ложное тогда, когда ложное хотя бы одно из утверждений.

Высказывание со словом «или» ложное тогда, когда ложны оба его утверждения.

Ребята, посмотрите, бабочка нам принесла книгу высказываний с красивыми картинками. И нам надо определить истинность высказываний.

Открываем первую страницу, внимательно смотрим на картинки и читаем первое высказывание.

На первой картинке торт и на второй картинке торт. Это составное высказывание, т.к. состоит из двух утверждений, которые соединены словом «и». Определим истинность этого высказывания. На первой картинке торт – это истинное утверждение, т.к. на первой картинке действительно торт. На второй картинке торт - это ложное утверждение, т.к. на второй картинке не торт, а мороженое. А мы знаем, что если в высказывании со словом «и» ложное хотя бы одно утверждение, то такое высказывание тоже ложное.

Значит, это высказывание ложное.

Открываем следующую страницу.

На первой картинке торт и на второй картинке торт. Определим истинность этого высказывания. На первой картинке торт – это истинное утверждение. На второй картинке торт – тоже истинное утверждение. А так как в высказывании со словом «и» истинные оба утверждения, то истинно само высказывание.

Давайте посмотрим на следующую картинку и высказывание.

На первой картинке арбуз или на второй картинке арбуз. Первое утверждение истинное, а второе ложное. Обратите внимание на то, что утверждения соединены словом «или». А мы знаем, что высказывание со словом «или» истинное, если истинное хотя бы одно из утверждений. Значит, наше высказывание истинное.

Следующая страница.

На первой картинке обувь и на второй картинке обувь. Конечно это высказывание ложное, т.к. ложные оба его утверждения.

И последняя страница.

На первой картинке не обувь или на второй картинке не одежда. Обратите внимание, в этом высказывании появилось отрицание, т.к. появилось слово «не». Но, мы сможем определить истинность и такого высказывания. Определяем истинность первого утверждения: на первой картинке не обувь – это истинное утверждение, т.к. на первой картинке действительно не обувь. Второе утверждение: на второй картинке не одежда – и это истинное утверждение, т.к. действительно на второй картинке не одежда. Значит, если оба утверждения истинные, то и всё высказывание истинное.

Мы определили истинность всех высказываний, закрываем книгу и смотрите, бабочка написала, что мы уже готовы сделать выводы из нашего урока.

Ребята, волшебная бабочка сегодня познакомила нас с составными высказываниями. Это высказывания, которые состоят из нескольких утверждений. Эти утверждения могут соединяться словами «и», «или».

Чтобы определить истинность составного высказывания, необходимо определить истинность каждого утверждения.

А давайте составим таблицу истинности высказываний со словами «и», «или».

Мы помним, что истинные утверждения будем обозначат буквой И, а ложные – буквой Л.

Итак!

Если в составном высказывании со словом И истинные оба утверждения, то и всё высказывание истинное.
Если в составном высказывании со словом И ложное хотя бы одно из ут­верждений, то и всё высказывание ложное.

Если в составном высказывании со словом ИЛИ истинное хотя бы одно из утверждений, то и всё высказывание истинное.

Если в составном высказывании со словом ИЛИ ложные оба утверждения, то и всё высказывание ложное.

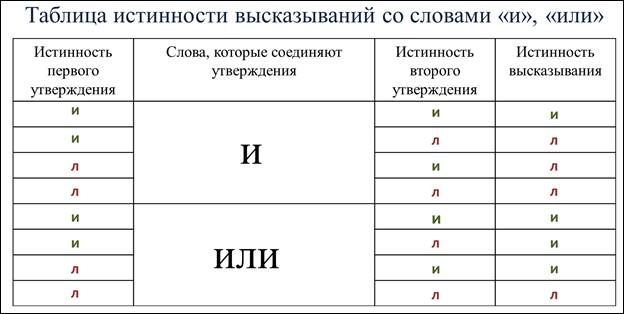
Таблица истинности готова. Выводы сделаны. А я желаю вам удачи и отличных отметок.