Системы неравенств с двумя переменными

Решением неравенства с двумя переменными называется пара значений переменных, обращающие данное неравенство в верное числовое неравенство.

Определение:

Решением системы неравенств называются пара значений переменных, обращающая каждое неравенство системы в верное числовое неравенство.

Проверим, являются ли решениями системы пары чисел. Система состоит из двух неравенств, подставим значения в систему:

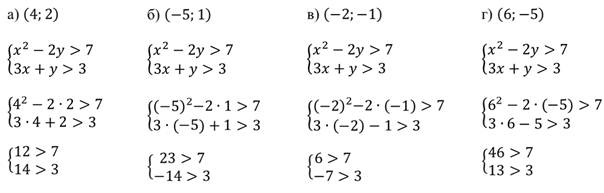
Получаем, что пара чисел системы а) и г) являются решениями, а пара чисел системы б) и в) - не являются решениями.

Понятно, что если каждое неравенство может иметь множество решений, то и общих решений может найтись большое количество.

Изобразим на координатной плоскости множество решений системы неравенств:

Найдём множество решений первого неравенства:

Изобразим график:

Решением будет множество точек расположенных ниже прямой.

Найдём множество решений второго неравенства:

Изобразим график уравнения:

Решением будет множество точек расположенных ниже прямой.

Изобразим множества решений неравенств в одной координатной плоскости:

Видим их общие решения, которые являются решением системы неравенств.

Изобразим на координатной плоскости множество решений системы неравенств:

Изобразим множество решений первого неравенства:

Изобразим график уравнения:

Решением неравенства будет множество точек находящихся ниже прямой.

Перейдём ко второму неравенству системы:

Изобразим график:

Решением неравенства будет множество внутренних точек круга.

Пересечение полученных множеств и является решением данной системы неравенств.

Изобразим на координатной плоскости множество решений системы неравенств:

Решением первого неравенства будет множество внутренних точек круга:

Решением второго неравенства будет множество, состоящее из точек, находящихся вне круга.

Пересечение полученных множеств и является решением данной системы:

Изобразим на координатной плоскости множество решений системы неравенств:

Изобразим множество решений ещё одной системы неравенств.

Решением первого неравенства будет множество точек находящихся между ветвями гиперболы. Решением второго неравенства будет множество внутренних точек круга.

Фигура, полученная в результате пересечения двух решений, представляет собой множество решений данной системы.