Неравенства с двумя переменными

Рассмотрим неравенство:

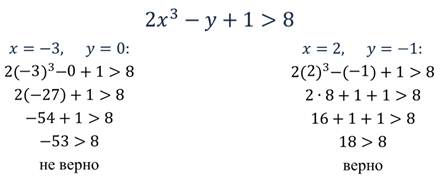
Определение:

Решением неравенства с двумя переменными называется пара значений этих переменных, обращающая данное неравенство в верное числовое неравенство.

Тогда пара значений (2; -1) является решением данного неравенства, но это не единственное решение.

Пример.

Проверить, является ли пара чисел (-2; 3) решением неравенств.

Подставим пару этих значений в каждое неравенство и проверим, обратятся ли они в верные числовые неравенства:

Получили, что в первом и во втором случаях - верное неравенство, а в третьем - пара чисел (-2; 3) не является решением данного неравенства.

Пример.

Найти два каких-нибудь решения неравенства:

Очевидно, что х может быть любым числом.

Например:

Среди множества решений данного неравенства будут пары чисел: (5; 17) и (-3; 8).

Так как неравенство с двумя переменными имеет множество решений, то их сложно перечислить. Увидеть множество решений неравенства с двумя переменными позволяет график.

Изобразим на координатной плоскости множество точек, заданных неравенством:

Построим график уравнения:

Графиком является прямая и для её построения достаточно двух точек:

Возьмём на прямой некоторую точку М с координатами (). Если мы возьмём точку К выше прямой, видно, что её абсцисса = , а вот ордината > . Тогда получаем, что координаты точки К не удовлетворяют неравенству. Если же взять точку, расположенную ниже прямой, с абсциссой = , то видно, что её ордината будем < . Тогда координаты этой точки будут удовлетворять неравенству:

Получили множество точек находящихся ниже.

Изобразим на координатной плоскости множество точек, заданных неравенством:

Изобразим график уравнения:

Возьмём на графике некоторую точку М с координатами ().  Если мы возьмём точку К выше графика, то видно, что её абсцисса = , а вот ордината > . Тогда получаем, что координаты точки удовлетворяют неравенству. Если же взять точку N, расположенную ниже графика, с абсциссой = , то видно, что её ордината будем < . Тогда координаты этой точки будут не удовлетворять неравенство:

Выберем нужное нам множество. Получаем:

Изобразим на координатной плоскости множество точек, заданных неравенством:

Изобразим график:

Взяв любую точку внутри окружности, можно увидеть, что её координаты удовлетворяют неравенству. Координаты точек, находящихся вне окружности не удовлетворяют неравенству.

Вернёмся к неравенству, решением будет являться множество точек находящихся внутри окружности и принадлежащих ей:

Изобразим на координатной плоскости множество точек, заданных неравенством:

Это уравнение обратной пропорциональности, графиком является гипербола. Составим таблицу значений:

 Отметим полученные точки на координатной плоскости и изобразим график:

Линии графика разделили координатную плоскость на три области. Координаты точек из области А будут удовлетворять неравенству. Координаты точек из области B не удовлетворяют неравенству. И если точка принадлежит области С, то точки этой области будут удовлетворять неравенству.

Множеством решений неравенства будут - А и С, включая линии графика.