Последовательности

Установить некоторую закономерность и дописать ещё одно число в каждый ряд.

В первом случае в порядке убывания записаны нечётные числа:

Во втором случае каждое следующее число отличается от предыдущего на 5:

В третьем случае:

Только что мы с вами привели примеры последовательностей, ещё их можно называть числовыми последовательностями.

Последовательности будем называть буквами, например , где n - количество членов последовательности.

Числа, образующие последовательность, называют членами последовательности.

Члены последовательности называют такой же буквой с указанием его порядкового номера n, где n является натуральным числом.

Например,  - множество положительных чётных чисел записанных в порядке возрастания. Члены последовательности - .

Такие последовательности называют бесконечными. Так как в названии последовательности не указано точное количество членов.

Так же последовательность может быть конечной.

Например, последовательность (): 2, 4, 6, 8, 10, имеет 5 членов последовательности, и её последний член равен 10.

Пример.

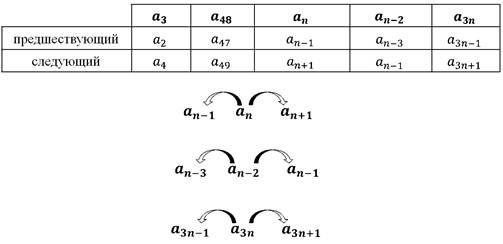
Для каждого члена последовательности , записать предшествующий ему и следующий за ним.

Формула n – ого члена:

Например:

Пример.

Найти первых пять членов последовательности, заданной формулой:

Найти пять первых членов последовательности, заданной формулой:

Нашли первых пять членов последовательности с помощью формулы. В данном случае, для нахождения каждого члена нам достаточно было знать только его номер.

Пример.

1.                Найти пять первых членов последовательности. Она задана первым членом

и формулой, выражающей каждый член последовательности через предыдущий:

Для нахождения последующих членов последовательности нужно:

Получили первых пять членов последовательности по первому члену и рекуррентной формуле.

2.                Найти пять первых членов последовательности. Она задана первым членом

и формулой, выражающей каждый член последовательности через предыдущий:

Для нахождения последующих членов последовательности нам нужно:

Получили первых пять членов последовательности по первому члену и рекуррентной формуле.