Вопросы занятия:
· познакомиться с понятием arccos;
· вывести общую формулу решения уравнений вида cos t = a.
Материал урока.
Прежде чем приступить к изучению нового материала, давайте выполним упражнение.
Упражнение.

Рассмотрим волну графика функции y = cos x на промежутке [0; π]. Отметим на оси абсцисс точки кратные π/6. А на оси ординат отметим соответствующие им значения функции. Отметим точки кратные π/4 и соответствующие им значения функции.

Промежуток [0; π] был выбран нами неслучайно.

Мы знаем, что если задана функция, то всегда можно решить две задачи: прямую (зная аргумент найти значение функции) и обратную (зная значение функции найти значение аргумента).
То, что функция монотонно убывает на данном промежутке, позволяет нам утверждать, что решение обратной задачи будет единственным.
Когда мы с вами составляли табличные значения косинуса, то мы брали основные точки первого и второго макета. И для них мы легко можем решить обратную задачу. А что же делать с другими значениями косинуса из промежутка [-1; 1]?
Например, найд`м значение аргумента, при котором y = y1. Очевидно, что y1 находится в промежутке [0; 0,5], соответственно, x1 будет находится в промежутке [π/3; 3π/2]. А как его определить?
Для таких случаев было введено специальное название арккосинус.

Обратите внимание, что арккосинусом любого числа является угол.

Сформулируем основное свойство арккосинуса.

Решим несколько типовых задач.
Задача.

Задача.

Задача.

Рассмотрим пример.
Пример.


Решим уравнение cos t = a, где а принадлежит отрезку [-1; 1] в общем виде.

Рассмотрим несколько частных случаев уравнения cos t = a.



Рассмотрим пример.
Пример.

Давайте ещё раз сформулируем алгоритм решения тригонометрических уравнений вида cos t = a.

Рассмотрим пример.
Пример.


 Получите свидетельство
Получите свидетельство Вход
Вход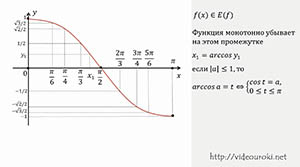



 0
0 4316
4316

