Вопросы занятия:
· познакомиться с понятием arcsin;
· вывести общую формулу решения уравнений вида sin t = a.
Материал урока.
Прежде чем перейти к изучению нового материала, давайте выполним несколько упражнений.
Упражнение.

Напомним ещё раз, что же называется arccos a.

Сегодня на уроке, мы познакомимся с понятием arcsin и научимся решать простейшие тригонометрические уравнения вида sin t = a, где а принадлежит промежутку [-1; 1].
Функцию arccos мы вводили как обратную функцию для функции cos t. Аналогично, введём функцию arcsin a. Для того, чтобы на некотором промежутке существовала обратная функция, необходимо, чтобы функция была непрерывна и монотонна на этом промежутке.
Для функции y = sin x таким промежутком будет являться промежуток [-π/2; π/2]. На этом промежутке функция синус непрерывна, монотонна и принимает все значения из своей области значений.
Давайте теперь сформулируем определение арксинуса в общем виде.

Обратите внимание, что арксинусом любого числа является угол.

Сформулируем основное свойство арксинуса.

Отметим важное равенство, связывающее arccos a и arcsin a, из промежутка [-1; 1].

Введённое понятие арксинуса, помогает решать уравнение вида sin t = a, где а не является табличным значением и принадлежит отрезку [-1; 1].
Рассмотрим пример.
Пример.

Решим уравнение sin t = a, модуль которого не превышает единицы в общем виде.

Рассмотрим частные случаи решения тригонометрического уравнения sin t = a.



Рассмотрим пример.
Пример.

Давайте ещё раз сформулируем алгоритм решения тригонометрических уравнений вида sin t = a.

Давайте рассмотрим более сложное уравнение и постараемся его привести к простейшему уравнению sin t = a.
Рассмотрим пример.
Пример.

Итак, в результате мы получили формулы корней для уравнений cos t = a и sin t = a, при условии, что модуль а не превышает единицы.

Переменную мы пока обозначали буквой t для удобства, подчёркивая тем самым, что вся информация получена с помощью числовой окружности. Но когда имеется готовая формула, переменная может быть обозначена любой буквой, в том числе более традиционной для уравнений буквой x. Так мы чаще всего и будем поступать при решении тригонометрических уравнений.

 Получите свидетельство
Получите свидетельство Вход
Вход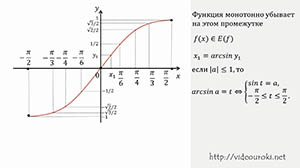



 0
0 4215
4215


