В курсе геометрии 8 класса, мы с вами уже знакомились с понятиями синуса, косинуса, тангенса и котангенса для углов прямоугольного треугольника. Давайте вспомним их.
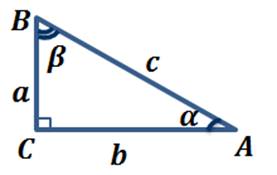
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
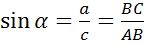
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
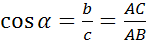
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
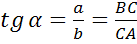 ;
; 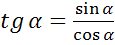
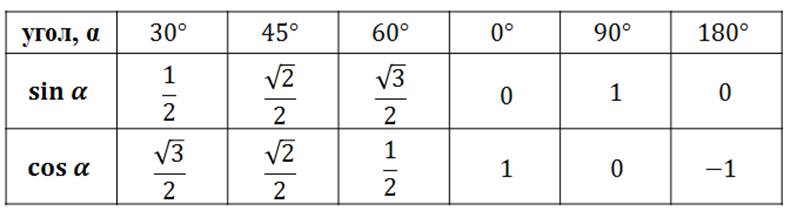
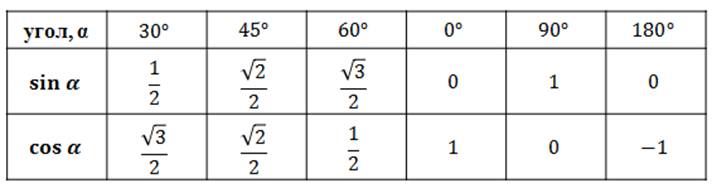
Еще мы с вами учили таблицу синусов, косинусов для углов в 30, 45 и 60 градусов. Давайте вспомним ее.
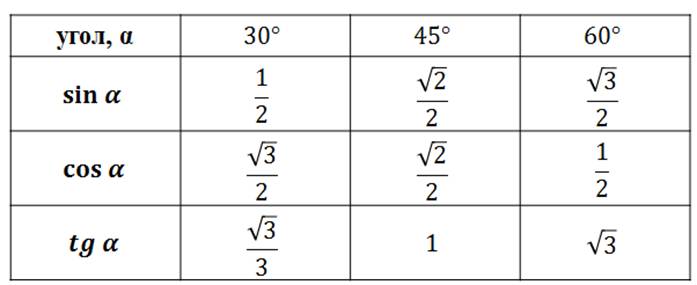
Сегодня на уроке мы познакомимся с понятиями синуса, косинуса, тангенса и котангенса произвольного угла из промежутка от 0 до 180º.
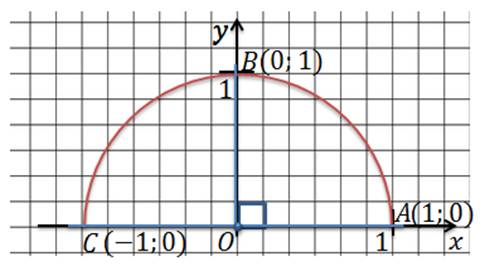
Построим в прямоугольной системе координат полуокружность радиус которой равен 1 так, чтобы центр этой полуокружности совпадал с началом координат.
Такую полуокружность мы назовем единичной полуокружностью. Из точки О давайте проведем произвольный луч h. Этот луч пересекает полуокружность с точке М (0;0). Угол между лучом h и положительным направлением оси Ox обозначим за α. Если луч h совпадает с положительным направлением оси Ox, то угол α равен 90º. Если луч h совпадает с осью Oy, то угол α= 90º. Если луч h совпадает с отрицательным направлением оси Ox, то угол α= 180º. Опустим из точки М перпендикуляр на ось Ox и рассмотрим прямоугольный треугольник ОМD.
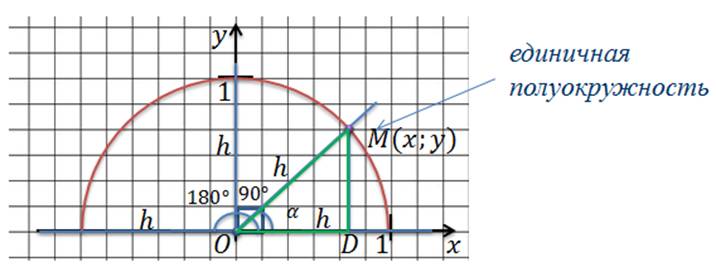
Запишем элементы этого треугольника. Поскольку радиус полуокружности
равен 1, значит, ОM=1. Так как координаты точки М равны
x и y, то, очевидно, что МD=y, а ОD=x. Тогда 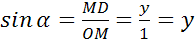 ,
, 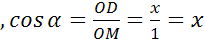 . Мы
получили, что синус острого угла равен ординате точки М, а косинус угла α
равен абсциссе точки М. По этим же формулам вычисляются синус и косинус для
углов в 90º и 180º.
. Мы
получили, что синус острого угла равен ординате точки М, а косинус угла α
равен абсциссе точки М. По этим же формулам вычисляются синус и косинус для
углов в 90º и 180º.
Для любого угла 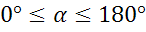 синусом
угла
синусом
угла 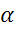 называется
ордината
называется
ордината 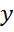 точки
точки
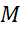 , а косинусом
угла
, а косинусом
угла 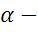 абсцисса
абсцисса
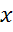 точки
точки
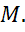
Поскольку речь у нас идет о единичной полуокружности, то ордината точки может изменятся от 0 до 1, значит, и синус угла α может принимать значения от 0 до 1. Абсцисса точки М может изменятся от -1 до 1, то есть и косинус угла α из промежутка от 0 до 180º может изменятся от -1 до 1.
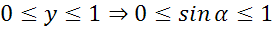
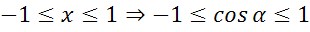
Задача. Может ли:
а) абсцисса точки единичной полуокружности быть равна 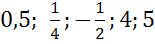 ?
?
б) ордината точки единичной полуокружности быть равна 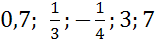 ?
?
Решение.
а) Поскольку полуокружность единичная, значит абсцисса точки должны
принадлежать промежутку от -1 до 1, то есть абсцисса точки может быть равна 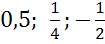 , но не
может быть равна 4 и 5.
, но не
может быть равна 4 и 5.
б) Поскольку полуокружность располагается выше оси Ox,
то ординаты точек могут быть только из промежутка от 0 до 1, то есть ордината
точки может быть равна 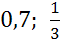 но не
может быть равна
но не
может быть равна 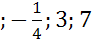 .
.
Дополним известную нам таблицу синусов косинусов:
Для определения sin 0º и cos 0º давайте рассмотрим луч ОА. На единичной
полуокружности точка А имеет координаты (1;0), значит 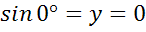 , а
, а 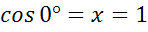 .
.
Найдем теперь значение sin90 º и cos 90º. Этот угол задается лучом ОB.
Координаты точки B равны (0;1), значит, 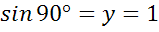 ,
, 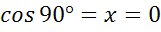 .
.
Проводя аналогичные рассуждения, получим 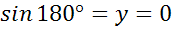 ,
, 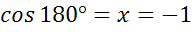 .
.
Задача. Определить координаты точки 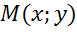 , если:
, если:
а) 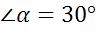 ; б)
; б) 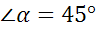 ; в)
; в) 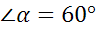 .
.
Решение.
а) 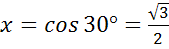
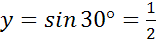
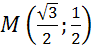
б) 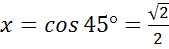
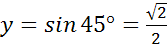
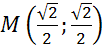
в) 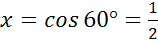
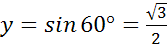
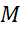
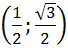
Ответ: 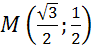 ;
; 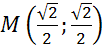 ;
; 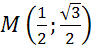 .
.
Решим теперь обратную задачу.
Задача. Определить 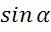 ,
, 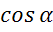 , если:
, если:
а) 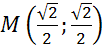 ; б)
; б) 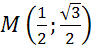 ; в)
; в) 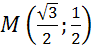 .
.
Решение.
а) 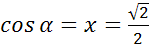
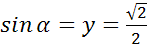
б) 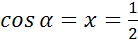
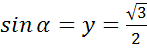
в) 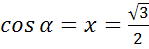
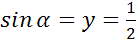
Тангенсом острого угла мы называли отношение
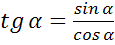 . Эта же
формула справедлива для произвольного угла от 0º до 180º. Однако,
если угол равен 90º, то его cos 90º=0, а
значит, мы получим дробь, в знаменателе которой находится 0. Но на 0 делить
нельзя, поэтому для угла в 90º тангенс не существует. Таким образом, мы
немного уточнили определение тангенса.
. Эта же
формула справедлива для произвольного угла от 0º до 180º. Однако,
если угол равен 90º, то его cos 90º=0, а
значит, мы получим дробь, в знаменателе которой находится 0. Но на 0 делить
нельзя, поэтому для угла в 90º тангенс не существует. Таким образом, мы
немного уточнили определение тангенса.
Тангенсом угла 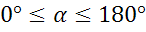 ,
, 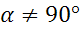 называется
называется
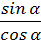 .
.
Котангенсом острого угла мы называли отношение 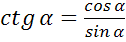 . Эта же
формула справедлива для произвольного угла от 0º до 180º. Однако,
если угол равен 0º или 180º, то sin равен 0,
а значит, мы получим дробь, в знаменателе которой находится 0. Но на 0 делить
нельзя, поэтому
. Эта же
формула справедлива для произвольного угла от 0º до 180º. Однако,
если угол равен 0º или 180º, то sin равен 0,
а значит, мы получим дробь, в знаменателе которой находится 0. Но на 0 делить
нельзя, поэтому
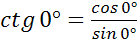 ,
, 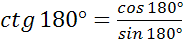 – не существует. Таким образом, мы немного уточнили
определение котангенса.
– не существует. Таким образом, мы немного уточнили
определение котангенса.
Котангенсом угла 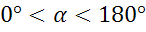 , называется
, называется
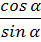 .
.
Задача. Определить 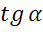 ,
, 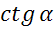 , если:
, если:
а) 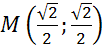 ; б)
; б) 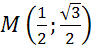 ; в)
; в) 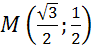 ; г)
; г) 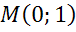 ; д)
; д) 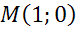 .
.
Решение.
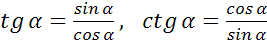
а) 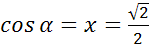
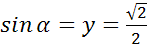
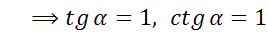
б) 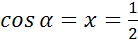
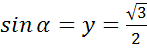
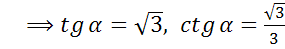
в) 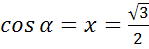
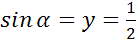
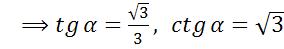
г) 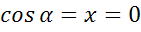
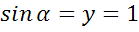
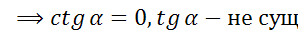
д) 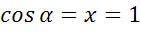
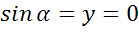
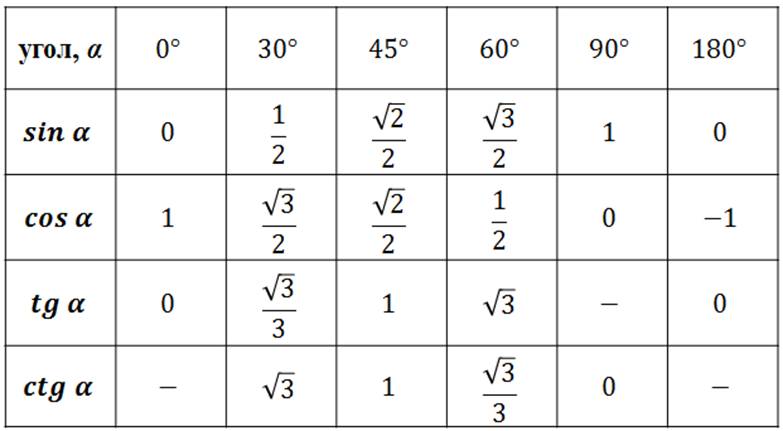
Давайте занесем полученные данные в таблицу и составим таблицу синусов, косинусов, тангенсов и котангенсов для углов 0º, 30º, 45º, 60º, 90º, 180º.
Подведем итоги урока. Сегодня на уроке мы определили, что Для любого угла 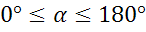 синусом угла
синусом угла 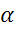 называется ордината
называется ордината 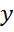 точки
точки 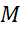 , а косинусом угла
, а косинусом угла 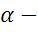 абсцисса
абсцисса 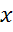 точки
точки 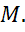
Тангенсом угла 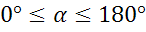 ,
, 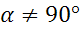 называется
называется
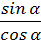 .
.
Котангенсом угла 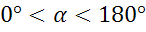 , называется
, называется
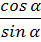 .
.
Также мы дополнили известную нам таблицу значений синуса, косинуса и тангенсов для некоторых углов.

 Получите свидетельство
Получите свидетельство Вход
Вход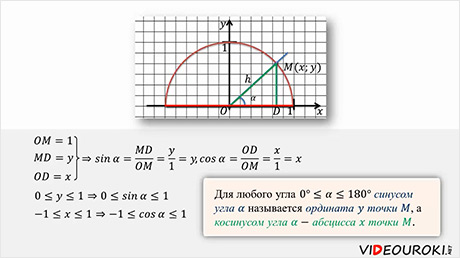



 0
0 22382
22382