Первый признак подобия треугольников

Вспомним, что подобными называются треугольники, у которых углы соответственно равны, а сходственные стороны пропорциональны.

На одном из предыдущих уроков мы отмечали, что подобие треугольников можно установить, проверив только некоторые из равенств. И сейчас мы познакомимся с первым признаком подобия треугольником.

Теорема (1-й признак подобия треугольников). Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.

Доказательство.

, .

, , ,

, следовательно, .

Так как , то .

Так как , то .

, .

Так как , то .

, .

Следовательно, .

Выше мы доказали, что соответственные углы этих треугольников равны, а значит, они треугольники подобны.

Что и требовалось доказать.

Из доказанной теоремы следует, что прямая, параллельная одной из сторон треугольника, отсекает от него треугольник, подобный данному.

Давайте возьмём некоторый треугольник ABC и проведём прямую MN, параллельную стороне AC.

 как соотв. при  и секущей ,  

 как соотв. при  и секущей , 

следовательно,  по 1-му признаку.

Также из доказанного признака следует, что прямоугольные треугольники подобны по острому углу.

Действительно. Если у прямоугольных треугольников ABC и A₁B₁C₁ угол А равен углу А₁, то  по 1-му признаку.

А теперь давайте посмотрим на следующие треугольники и найдём среди них подобные.

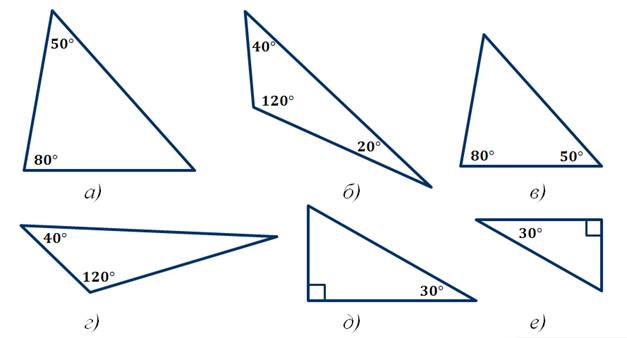
Итак, треугольники а и в подобны по первому признаку, так как два угла одного треугольника соответственно равны двум углам другого треугольника.

Треугольники д и е являются подобными, так как они прямоугольные и у них острые углы равны.

И у нас остались треугольники б и г. Так как сумма углов треугольника равна ста восьмидесяти градусам, то несложно найти градусную меру третьего угла треугольника б. Она равна 40º. А тогда эти треугольники подобны по двум углам, то есть по первому признаку.

Задача. На стороне  параллелограмма отмечена точка . Прямые  и  пересекаются в точке . Найдите  и , если  см,  см,  см,  см.

Решение.

Рассмотрим  и .

 как вертикальные,  как внутр. накрест лежащие  при  и секущей . 

Значит,  по 1-му признаку.

, то есть .

, ,  (см).

 см.

, ,  (см).

Ответ:  см;  см.

Задача. На рисунке  см,  см,  см, а . Найдите .

Решение.

Рассмотрим  и .

 по условию задачи,  – общий.  

Значит,  по 1-му признаку.

, ,   (см).

Ответ:  см.

Итак, на уроке мы доказали первый признак подобия треугольников: если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.

Убедились, что прямая, параллельная одной из сторон треугольника, отсекает от него треугольник, подобный данному. А также, что прямоугольные треугольники подобны по острому углу.

Кроме этого решили задачи на закрепление нового материала.