На прошлом уроке мы с вами говорили, что подобными называются треугольники, у которых углы соответственно равны, а сходственные стороны пропорциональны.
Число k, равное отношению сходственных сторон подобных треугольников, называется коэффициентом подобия.
Напомним, что подобие треугольников обозначается
следующим образом  .
.
На этом уроке мы докажем теорему об отношении площадей двух подобных треугольников.
Теорема. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Доказательство.

 ,
,
 –
коэффициент подобия.
–
коэффициент подобия.
 ,
,
 .
.
 ,
,
 .
.
 ,
,
 ,
,

Следовательно,  .
.
Что и требовалось доказать.
Задача. Площади подобных
треугольников  и
и
 равны
соответственно
равны
соответственно  см2
и
см2
и  см2.
Сторона
см2.
Сторона  см.
Найдите сходственную ей сторону
см.
Найдите сходственную ей сторону  треугольника
треугольника
 .
.
Решение.

Выше мы доказали, что отношение площадей двух
подобных треугольников равно квадрату коэффициента подобия.  ,
,  ,
,
 .
.
 ,
,
 ,
,
 (см).
(см).
Ответ:  см.
см.
Задача. Докажите, что отношение периметров двух подобных треугольников равно коэффициенту подобия.
Доказательство.
 ,
,
 –
коэффициент подобия.
–
коэффициент подобия.
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
 ,
,
 .
.
 ,
,
 ,
,
 .
.
Что и требовалось доказать.
Задача. Треугольники  и
и
 подобны.
Сходственные стороны
подобны.
Сходственные стороны  и
и
 соответственно
равны
соответственно
равны  см
и
см
и  м.
Найдите отношение периметров треугольников
м.
Найдите отношение периметров треугольников  и
и
 .
.
Решение:

 м
м см.
см.
 .
.
 .
.
Ответ:  .
.
Итак, на этом уроке мы доказали, что отношение площадей двух подобных треугольников равно квадрату коэффициента подобия. А также решили несколько задач. Причём при решении одной из них установили, что отношение периметров двух подобных треугольников равно коэффициенту подобия.

 Получите свидетельство
Получите свидетельство Вход
Вход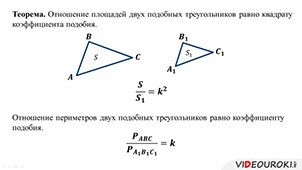



 0
0 22402
22402

