Пропорциональные отрезки. Определение подобных треугольников

При сравнении двух значений какой-то величины часто возникает вопрос:

во сколько раз одно значение больше другого? или какую часть по отношению к другому оно составляет?

Например, во сколько раз заяц пробежит быстрее некоторое расстояние, чем это же расстояние проползёт улитка? Или какую часть всех деревьев леса составляют берёзы?

Вы знаете, что ответ в таких случаях дается в виде частного двух чисел, которое называют отношением. Отношение показывает, во сколько раз первое число больше второго, или какую часть первое число составляет от второго.

Отношением отрезков  и  называется отношение их длин, т. е.  (или ).

Отрезки  и  пропорциональны отрезкам и , если .

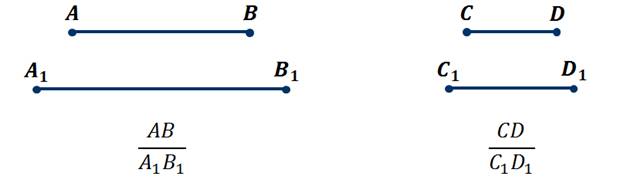
Например, отрезки AB и A₁B₁ равны соответственно 3 сантиметра и 5 сантиметров; а отрезки CD и C₁D₁ – соответственно сантиметра и 7,5  сантиметра.

;  

.

Отрезки  и  пропорциональны отрезкам и .

Следует отметить, что понятие пропорциональности справедливо и для большего количества отрезков. Например, отрезки AB, CD и EF пропорциональны отрезкам A₁B₁; C₁D₁ и E₁F₁, если справедливо равенство: .

А теперь давайте посмотрим на рисунок.

 Так, матрёшки имеют одинаковую форму, но разные размеры. То же самое можем сказать про футбольный и теннисный мячи, про одинаковые фотографии разных размеров.

В геометрии фигуры одинаковой формы называют подобными. Любые два квадрата и любые два круга являются подобными.

А какие два треугольника называют подобными? Возьмём два треугольника ABC и A₁B₁C₁, у которых угол А равен углу A₁, угол B равен углу B₁, а угол C равен углу C₁.

Тогда стороны AB и A₁B₁, BC и B₁C₁, AC и A₁C₁ называются сходственными. И если эти сходственные стороны пропорциональны , то треугольники ABC и A₁B₁C₁ являются подобными. Подобие треугольников обозначается следующим образом

Сформулируем определение: подобными называются треугольники, у которых углы соответственно равны, а сходственные стороны пропорциональны.

Отношение сходственных сторон называют коэффициентом подобия. Если стороны треугольника ABC в два раза больше сторон треугольника A₁B₁C₁, то отношение сходственных сторон равно 2, то есть коэффициент подобия равен 2.

Подобие треугольников можно установить, проверив только некоторые из равенств:

, т. е.

И позднее мы с вами познакомимся с тремя признаками подобия треугольников.

Решим несколько задач.

Задача. Найдите отношение отрезков  и , если их длины соответственно равны  см и  см. Изменится ли это отношение, если длины отрезков выразить в миллиметрах?

Решение.

 см мм,

 см мм.

.

Ответ: ; не изменится.

Задача. Пропорциональны ли отрезки  и , соответственно равные  см и  см, отрезкам  и , соответственно равным  см и  см?

Решение.

;

;

.

Ответ: пропорциональны.

Задача. В подобных треугольниках  и  стороны  и ,  и  являются сходственными. Найдите стороны треугольника  , если  см,  см,  см, а отношение сторон  .

Решение.

    то есть    (см).

     (см).

   (см).

Ответ:  см,  см,  см.

Итак, на уроке мы узнали, что отношением отрезков  и  называется отношение их длин, т. е.  (или ); что отрезки  и  пропорциональны отрезкам и , если .

Также мы выяснили, что подобными называются треугольники, у которых углы соответственно равны, а сходственные стороны пропорциональны.