Если вы когда-нибудь играли в разведчиков, то знаете, что в этой игре разведчик вынужден вести переписку со своими товарищами так, чтобы никто из посторонних не смог прочитать написанного. Для этого используют шифровки.
Познакомимся с одним из способов шифровки – способом решётки.
Возьмём квадрат из плотной бумаги, разделим его на 64 квадратика и прорежем 16 окошечек вот таким образом…

Представим, что вам необходимо передать сообщение соседу по парте, в котором зашифровано известное высказывание Михаила Васильевича Ломоносова: «Математику уже затем учить надо, что она ум в порядок приводит».
Михаил Васильевич Ломоносов – первый русский учёный-естествоиспытатель мирового значения. Яркий пример «универсального человека»: энциклопедист, химик и физик. Основоположник научного мореплавания и физической химии. Он заложил основы науки о стекле. Астроном (он открыл наличие атмосферы у планеты Венеры), приборостроитель, географ и геолог. Также поэт, художник, филолог.
Давайте наложим изготовленную нами решётку на листок бумаги. Будем писать сообщение в окошечках решётки.
Так как окошечек 16, то сначала помещается всего 16 букв: «Математику уже зат…»
Теперь поворачиваем решётку против часовой стрелки на 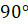 . Все написанные буквы закрыты. В новые окошечки мы продолжим
вписывать текст. Следующие 16 букв: «…ем учить надо, что он…»
. Все написанные буквы закрыты. В новые окошечки мы продолжим
вписывать текст. Следующие 16 букв: «…ем учить надо, что он…»
Снова поворачиваем решётку против часовой стрелки на 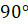 и вписываем в окошечки следующие 16 букв: «…а ум в порядок приво…»
и вписываем в окошечки следующие 16 букв: «…а ум в порядок приво…»
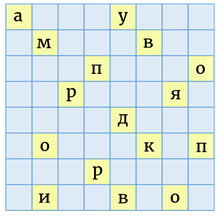
И остаётся вписать ещё 3 буквы.
Мы ещё раз поворачиваем решётку против часовой стрелки на 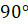 и вписываем оставшиеся 3 буквы: «…дит». У нас ведь остались
свободные клетки!
и вписываем оставшиеся 3 буквы: «…дит». У нас ведь остались
свободные клетки!
Если остаются неиспользованные клетки, то их заполняют буквами а, б, в и так далее (чтобы не было пробелов).
Заполним оставшиеся пустые клетки.
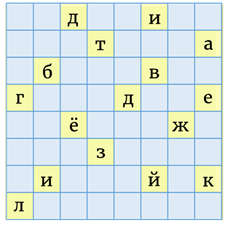
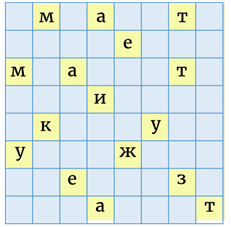
Таким образом, письмо принимает вот такой вид…

Такое письмо ни за что не прочесть человеку, который не имеет шифровального квадрата.
Читают такое письмо так же накладывая квадрат с окошечками и
поворачивая его против часовой стрелки на 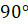 . А вот человеку, не имеющему шифровального квадрата, ни за что не
прочесть такое письмо.
. А вот человеку, не имеющему шифровального квадрата, ни за что не
прочесть такое письмо.
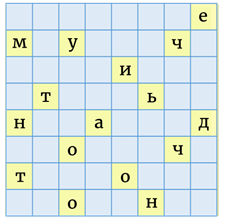
Давайте с помощью имеющейся решётки расшифруем вот такое письмо.

Итак, наложим решётку на текст. Выпишем буквы, которые появились в окошечках. Это будут первые 16 букв сообщения (Непереходитепрое).
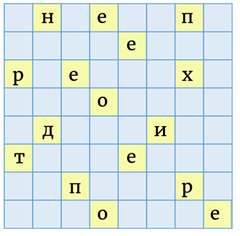
Затем повернём квадрат против часовой стрелки на 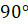 и увидим следующие 16 букв письма. Выпишем их (зжуючастьулицыпе).
и увидим следующие 16 букв письма. Выпишем их (зжуючастьулицыпе).
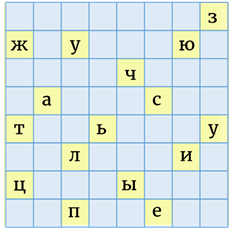
Снова повернём квадрат против часовой стрелки на 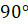 и выпишем 16 букв, которые появились в окошечках (редблизкоидущимт).
и выпишем 16 букв, которые появились в окошечках (редблизкоидущимт).
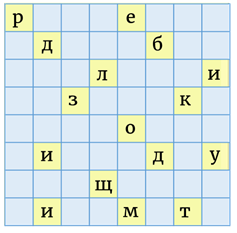
И четвёртый раз повернём квадрат на 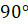 против часовой стрелки. Выпишем последние 16 букв (ранспортомабвгде).
против часовой стрелки. Выпишем последние 16 букв (ранспортомабвгде).
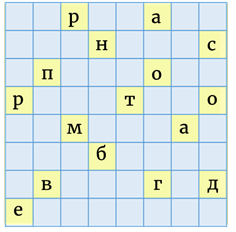
Теперь прочитаем, что у нас получилось: «Не переходите проезжую часть улицы перед близко идущим транспортом». И ещё остаются 6 букв (а, б, в, г, д, е).
Последние 6 букв использовались для того, чтобы в записке не оказалось пробелов.
Зашифровав одно сообщение и расшифровав другое, стало понятно, что способ шифровки основан на повороте квадрата вокруг его центра.
Поворот – это геометрическое
преобразование фигур, при котором свойства фигур не меняются, может измениться
лишь положение фигуры, так как каждая её точка повернётся вокруг некоторой
точки на угол поворота. Квадрат при повороте на 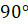 вокруг его центра совместится сам с собой.
вокруг его центра совместится сам с собой.
Каждая точка внутри квадрата при четырёх поворотах на 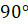 занимает 4 разных положения. «Окошечки» решётки займут в процессе
поворота 4 разных положения. Чтобы все клеточки
занимает 4 разных положения. «Окошечки» решётки займут в процессе
поворота 4 разных положения. Чтобы все клеточки 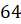 -клеточного квадрата были заполнены буквами, должно быть
-клеточного квадрата были заполнены буквами, должно быть 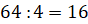 окошечек.
окошечек.
Вы можете изготовить свою решётку. Для этого надо разбить 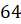 -клеточный квадрат, то есть размером
-клеточный квадрат, то есть размером 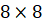 клеток, на 4 равные области (на 4 квадрата размером
клеток, на 4 равные области (на 4 квадрата размером 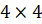 клетки). В первой области расставим числа от 1 до 16 в обычном
порядке.
клетки). В первой области расставим числа от 1 до 16 в обычном
порядке.
Вторая область получается из первой поворотом по часовой стрелке
на 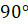 . Повернув ещё на
. Повернув ещё на 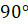 , получим заполнение третьей области. И, повернув последний раз,
получим заполнение четвёртой области.
, получим заполнение третьей области. И, повернув последний раз,
получим заполнение четвёртой области.
Затем выбирают для окошечек любые 16 клеток таким образом, чтобы в их числе не было клеток с одинаковыми номерами.
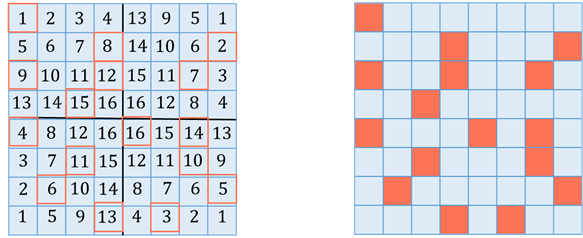
Итак, решётка готова, можете приступать к шифровке!
На 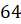 -клеточном поле можно составить более четырёх миллиардов секретных
решёток.
-клеточном поле можно составить более четырёх миллиардов секретных
решёток.
Давайте объясним этот факт. Итак, клетку номер 1 можно взять в
качестве окошка в четырёх местах. В каждом случае можно присоединить клетку
номер 2, взяв её также в четырёх местах. А значит, 2 окошка можно наметить 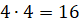 способами. 3 окошка можно наметить уже
способами. 3 окошка можно наметить уже 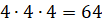 способами.
способами.
Продолжив дальше рассуждать таким способом, установим, что 16 окошек можно набрать числом способов, которое равно произведению шестнадцати четвёрок. Это число превышает 4 миллиарда.
Отметим, что если исключить решётки с примыкающими друг к другу окошками, то всё равно останется несколько сотен миллионов различных решёток.
Если бы возможна была только одна решётка, то способ переписки с её помощью совсем никуда не годился бы в смысле секретности.
Вместо квадратной решётки можно пользоваться и прямоугольной, в форме почтовой карточки, с широкими окошечками. В окошечки такой решётки вписывают не отдельные буквы, а части слов или даже целые слова, если они помещаются.
Не думайте, что запись окажется более разборчивой. Хотя отдельные слоги или слова окажутся видны, но перемешаны они будут в нелепом порядке, а секрет достаточно сохранён.
Существует множество различных способов зашифрованной переписки, но рассмотренный способ решётки очень близко соприкасается с математикой и ещё раз доказывает, как разнообразны стороны жизни, куда заглядывает эта наука.

 Получите свидетельство
Получите свидетельство Вход
Вход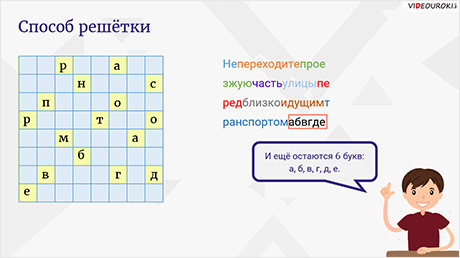




 6573
6573

