Здравствуйте, мальчики и девочки! Сегодня на занятии мы научимся решать задачи на взвешивание. Я думаю, что каждый из вас видел, как в магазине кладут товар на электронные весы, и на табло высвечиваются цифры, обозначающие массу товара. То есть взвешивать что-то с помощью электронных весов совсем несложно. Но если таких весов нет? И нет даже механических весов. А есть только чашечные весы и гири. Как поступить в такой ситуации?
Давайте рассмотрим вот такую задачу. Хозяйка собрала урожай яблок. Как ей отвесить 7 кг яблок для варенья, если у неё есть только чашечные весы и гиря массой 1 кг?
На одну чашу весов поставим килограммовую гирю. Вторую наполним яблоками так, чтобы чаши уровнялись. Таким образом, мы отмерили 1 кг яблок.
Далее возьмём гирю и переставим её на чашу с яблоками. Освободившуюся чашу наполним яблоками так, чтобы весы пришли в равновесие.
Сейчас у нас на одной чаше весов 1 кг яблок и килограммовая гиря. Вместе они весят 2 кг. Весы находятся в равновесии, а значит, на другой чаше – 2 кг яблок.
Переложим эти 2 кг яблок на чашу с 1 кг яблок и килограммовой гирей. Всё это весит 4 кг. Освободившуюся чашу наполним яблоками так, чтобы весы пришли в равновесие.
Теперь на одной чаше весов 4 кг яблок, а на другой – 3 кг яблок и килограммовая гиря. Следовательно, всего на весах 7 кг яблок.
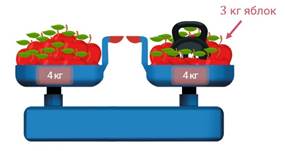
Друзья, вот таким образом, при помощи чашечных весов и килограммовой гири всего за 3 взвешивания хозяйка может отвесить 7 кг яблок для варенья.
Решим вторую задачу. На одной чаше весов лежат 4 одинаковых яблока и 2 одинаковых апельсина, на другой чаше – 2 таких же яблока и 3 таких же апельсина. Весы находятся в равновесии. Что тяжелее: яблоко или апельсин?
Итак, на одной чаше весов лежат 4 одинаковых яблока и 2 одинаковых апельсина. На другой – 2 таких же яблока и 3 таких же апельсина. Обратите внимание, что весы находятся в равновесии.

Чтобы ответить на вопрос задачи, давайте с каждой чаши весов снимем по 2 яблока и по 2 апельсина. На одной чаше весов осталось 2 яблока, а на другой – 1 апельсин. При этом весы по-прежнему находятся в равновесии, ведь с каждой чаши мы убрали фрукты одинаковой массы. А значит, 2 яблока весят столько же, сколько весит 1 апельсин. Очевидно, что апельсин тяжелее яблока.
Третья задача. 2 яблока и 1 груша весят столько, сколько 11 абрикосов. 5 абрикосов и 1 яблоко весят столько, сколько 1 груша. Сколько абрикосов нужно взять, чтобы уравновесить 1 грушу?
На одной чаше весов лежат 2 яблока и 1 груша, а на другой – 11 абрикосов. Весы находятся в равновесии.

Известно, что 5 абрикосов и 1 яблоко весят столько же, сколько 1 груша. Давайте заменим на весах 1 грушу пятью абрикосами и одним яблоком.

Видим, что 3 яблока и 5 абрикосов весят столько же, сколько 11 абрикосов.
Уберём с каждой чаши весов по 5 абрикосов и получим, что 3 яблока и 6 абрикосов весят одинаково. А значит, 1 яблоко по весу равно 2 абрикосам.
В задаче спрашивается, сколько абрикосов нужно взять, чтобы уравновесить 1 грушу. Так как 1 груша весит столько же, сколько 5 абрикосов и 1 яблоко, а 1 яблоко весит столько же, сколько 2 абрикоса, то, следовательно, 1 груша весит столько же, сколько 7 абрикосов.
Ответ: чтобы уравновесить 1 грушу, надо взять 7 абрикосов.
Ребята, теперь решим задачу, в которой будем взвешивать монеты.
Итак, среди трёх одинаковых на вид монет есть одна фальшивая, которая легче настоящей. За сколько взвешиваний на чашечных весах без гирь можно определить, какая монета является фальшивой?
Положим на каждую чашу весов по одной монете. Третью монету отложим в сторону. Если весы в равновесии, то монеты на них одинаковые, а значит, ни одна из них не фальшивая. Следовательно, фальшивая та монета, которую отложили в сторону.
Если же весы не в равновесии, то монета, с которой чаша весов поднялась выше, фальшивая, так как в условии задачи сказано, что она легче настоящей. Таким образом, получается, что всего за одно взвешивание можно определить, какая из трёх монет является фальшивой.
Ещё одна задача. Среди девяти одинаковых на вид монет есть одна фальшивая, которая легче, чем настоящая. Как за два взвешивания на чашечных весах без гирь определить фальшивую монету?
Разделим все монеты на группы по 3 штуки. Получились 3 такие группы.
Сначала кладём на каждую чашу весов по 3 монеты. Если весы в равновесии, то все монеты одинаковые, а значит, среди них нет фальшивой.
Тогда откладываем монеты, которые мы взвесили, и кладём на чаши весов по одной монете из третьей группы. Если весы в равновесии, то фальшивая монета, которая по условию задачи легче остальных, осталась лежать в стороне. Если же весы не в равновесии, то та монета, которая легче, является фальшивой. Таким образом, всего за 2 взвешивания можно определить, какая из девяти монет – фальшивая.
Если весы не были в равновесии при первом взвешивании, то для второго взвешивания берём группу монет, которая оказалась легче, то есть с которой чаша весов поднялась выше.
Друзья, на этом время, отведённое на нашу встречу, заканчивается. Пора прощаться. До свидания. До новых встреч.

 Получите свидетельство
Получите свидетельство Вход
Вход




 1624
1624

