Площадь трапеции

На этом уроке мы рассмотрим вопрос о вычислении площади трапеции.

Давайте вспомним  одно из свойств площадей: если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.

Также вспомним, что высотой трапеции называется перпендикуляр, проведённый из любой точки одного из оснований на другое основание или его продолжение.

А теперь докажем, что площадь трапеции равна произведению полусуммы длин её оснований на высоту.

Доказательство

Рассмотрим трапецию .

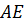 – высота.

Докажем, что .

,

.

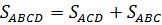
Так как ,

то .

,

.

Что и требовалось доказать.

Для закрепления решим несколько задач.

Задача. Найдите площадь трапеции , если  см,  см,  см, а .

Решение

Рассмотрим прямоугольный .

,

 (см).

,

 (см²).

Ответ:  см².

Задача. Градусная мера острого угла прямоугольной трапеции равна 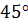, а высота, проведённая из вершины тупого угла, делит трапецию на треугольник и квадрат, площадь которого равна  см². Вычислите площадь трапеции.

Решение.

 Пусть ABCD – прямоугольная трапеция. Градусная мера острого угла C равна 45º. Высота BE, проведённая из тупого угла B делит трапецию на квадрат ABED и треугольник BCE.

Из условия задачи известно, что  см², значит,  (см).

 – прямоугольный,  так как  – высота.

,

,

.

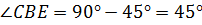 – равнобедренный.

 (см).

,  (см).

,

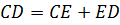 (см²).

Ответ:  см².

Итак, на этом уроке мы доказали, что площадь трапеции  равна произведению полусуммы длин её оснований на высоту. А также закрепили это на практике.