Логарифмические уравнения

Вопросы занятия:

• рассмотреть логарифмические уравнения;

• познакомить с основными методами их решения;

• рассмотреть подробные примеры решения логарифмических уравнений.

Материал урока

Прежде чем приступить к решению уравнений давайте повторим необходимые теоретические сведения.

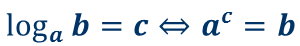
Запишем основное логарифмическое тождество.

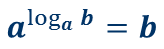
Повторим теорему, с помощью которой мы будем решать логарифмические уравнения.

Теперь давайте определим, какие уравнения называются логарифмическими. Логарифмическими уравнениями называют уравнения вида:

Можно сформулировать следующее утверждение.

Теорема.

Рассмотрим пример.

Рассмотрим еще один пример.

Рассмотрим еще один пример.

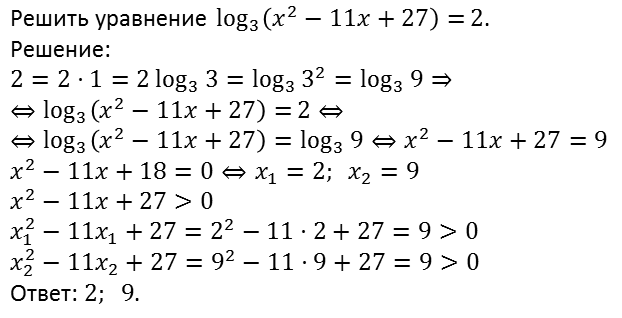
Рассмотрим еще один пример.

Рассмотрим еще один пример.

Рассмотрим еще один пример.

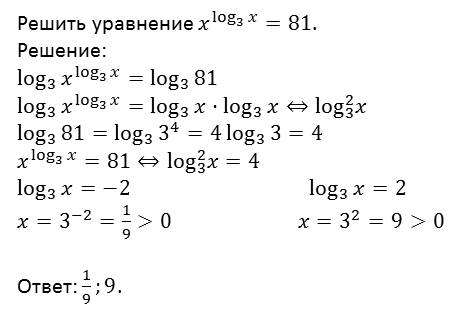
Рассмотрим еще один пример.

Давайте попробуем сформулировать алгоритм решения логарифмических уравнений.

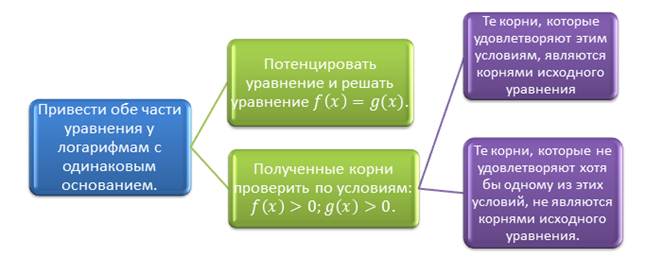
Теперь давайте определим, какие же методы решения логарифмических уравнений мы знаем.

Функционально-графический метод. Этот метод мы применяли при введении понятия логарифма и изучении свойств логарифмической функции. Он основан на использовании графических иллюстраций или каких-либо свойств функции.

Метод потенцирования. На сегодняшнем уроке большинство примеров мы решали именно с применением этого метода.

Метод введения новой переменной. Этот метод мы применяли при решении этого уравнения:

И еще один метод – метод логарифмирования, его мы применяли для решения этого уравнения: