Вопросы занятия:
· рассмотреть свойства логарифмов;
· подробно рассмотреть примеры, в которых необходимо преобразовать выражения с логарифмами.
Материал урока
Прежде чем приступить к изучению новой темы, давайте повторим определение логарифма, основное логарифмическое тождество:


Эти знания нам пригодятся на сегодняшнем уроке.
Сегодня мы рассмотрим основные свойства операции логарифмирования. Заметим, что все свойства мы будем формулировать только для положительных значений переменных, содержащихся под знаком логарифма.
Итак, первое свойство формулируется следующей теоремой:
Теорема 1.
Логарифм произведения двух положительных чисел равен сумме логарифмов этих чисел, то есть справедлива следующая формула:

Давайте докажем эту теорему.
Введём следующие обозначения.

Нам надо доказать, что выполняется равенство:

Применим определение логарифма.

По свойству произведения степеней с одинаковыми основаниями получим:

Поскольку степени двух положительных чисел равны и основания степеней равны и отличны от единицы, то равны и показатели степеней. Значит:

Что и требовалось доказать.
Рассмотрим пример.
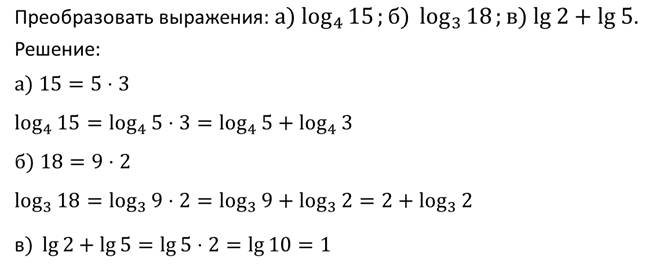
Сформулируем следующее свойство логарифмов.
Теорема 2.
Если а, b, c – положительные числа, причём a ≠ 1, то справедливо равенство:

Другими словами, логарифм частного равен разности логарифмов делимого и делителя.
Или: логарифм дроби равен разности логарифмов числителя и знаменателя.
Эта теорема доказывается аналогично предыдущей. Поэтому вы можете доказать её самостоятельно, воспользовавшись свойствами степеней.
Рассмотрим пример.

Сформулируем следующее свойство.
Теорема 3.
Если а и b – положительные числа, причём, a ≠ 1, то для любого числа r справедливо равенство:

Другими словами, логарифм степени равен произведению показателя степени на логарифм основания степени.
Эта теорема доказывается аналогично предыдущим, поэтому вы можете доказать её самостоятельно, воспользовавшись свойствами степеней.
Рассмотрим пример.
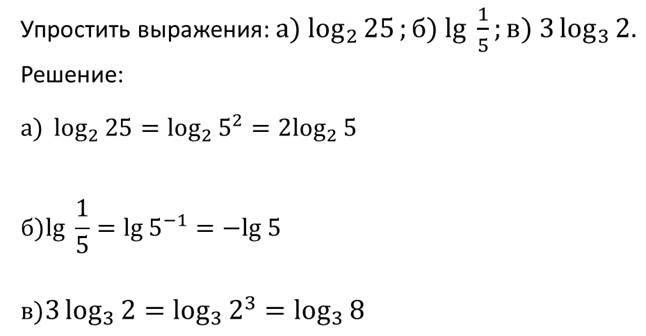
Сформулируем следующее свойство.
Свойство.
Если а и b – положительные числа, причём, a ≠ 1, то для любого числа r справедливо равенство:

Другими словами: логарифм, основанием которого является степень числа а равен произведению единицы делённой на показатель степени и логарифма числа b по основанию а.
Эта теорема доказывается аналогично предыдущим, поэтому доказывать её мы не будем.
Рассмотрим пример.

Рассмотрим ещё один пример.
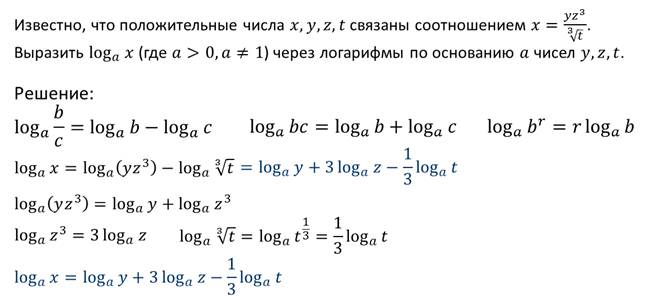
То есть нам удалось логарифм достаточно громоздкого выражения представить в виде суммы и разности логарифмов простых выражений. Такое преобразование называют логарифмированием. Иногда приходиться решать обратную задачу: находить выражение, логарифм которого представлен через логарифмы некоторых чисел. Такое действие называется потенцированием. При этом используют следующее утверждение:
Теорема 4.
Равенство:

справедливо тогда и только тогда, когда

Это утверждение следует из монотонности логарифмической функции.
Рассмотрим пример.

Ещё раз обратите внимание, что все свойства логарифмов мы получили при условии, что переменные принимают положительные значения. А как быть, если про знак переменной ничего неизвестно?
Например, можно ли записать:

Нет, нельзя, поскольку:

Правильнее будет записать так:


Мы должны помнить и о том, что:

только в том случае, когда b > 0 и с > 0. Если мы в этом не уверены, но знаем, что произведение bc > 0, то, поскольку в этом случае выполняется равенство:

то следует использовать формулу:

Рассмотрим ещё несколько примеров.
Пример.

Пример.

Пример.

Пример.
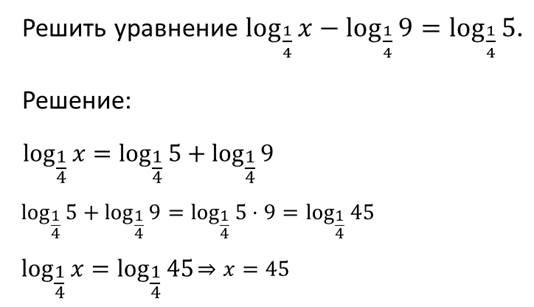
Итак, повторим основные свойства логарифмов:


 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 8320
8320